Предмет: Алгебра,
автор: chekashkin92
Самостоятельная работа по тебе "Производные"
Приложения:
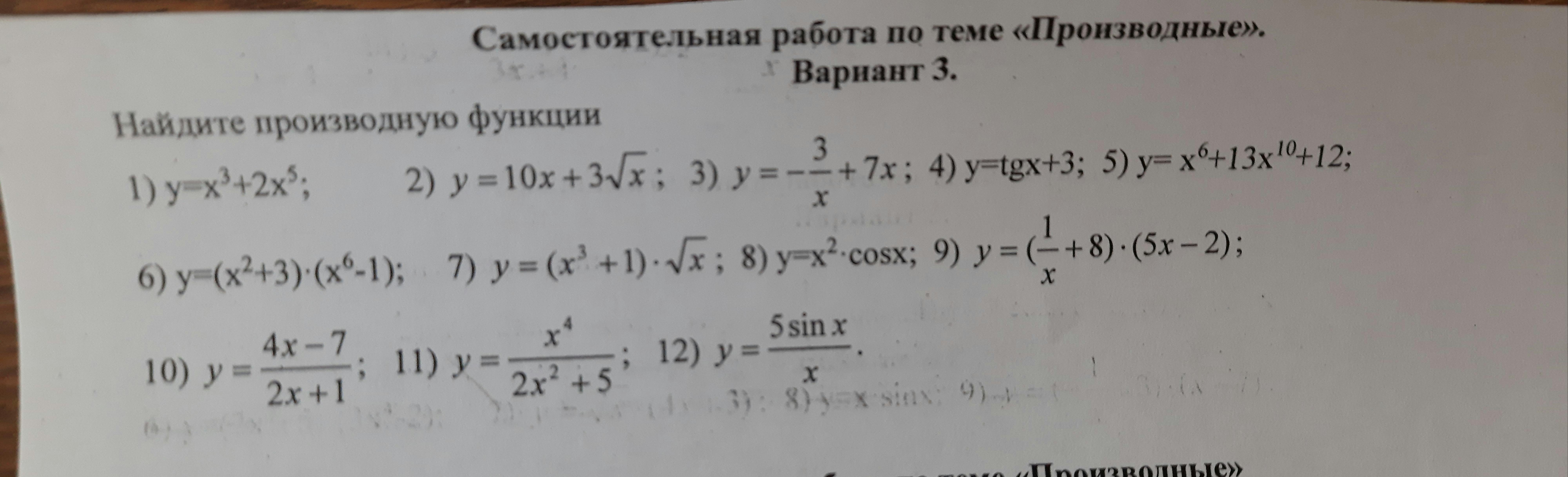
Ответы
Автор ответа:
1
chekashkin92:
Спасибо большое, но надо с полным решением
тебе, может, таблицу производных написать ??? это табличные производные ...
Похожие вопросы
Предмет: Математика,
автор: xxxirishkaxxx8
Предмет: Математика,
автор: adrusu12
Предмет: Русский язык,
автор: lerago
Предмет: Химия,
автор: ira121077
Предмет: Литература,
автор: Нилайн