Предмет: Математика,
автор: MolkyWay
Ребята! СРОЧНО! Помогите!
Приложения:
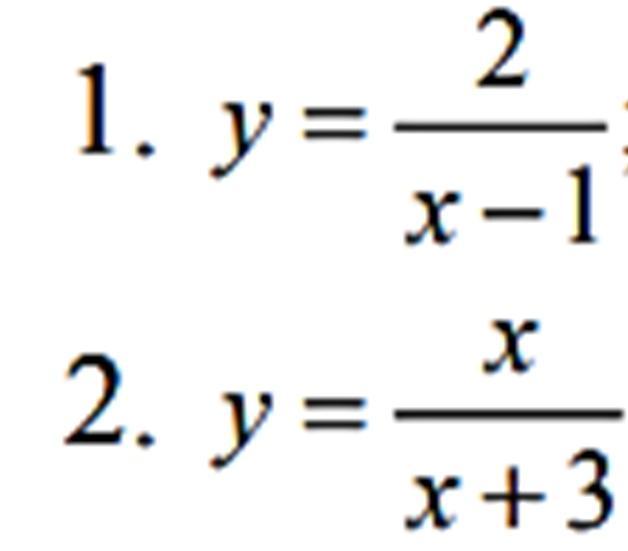
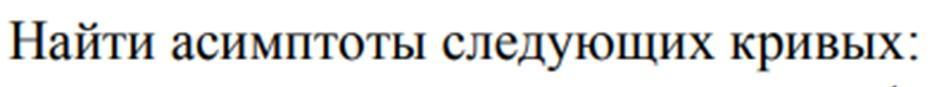
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
наклонную асимптоту ищем в виде k = ax +b
по определению асимптоты
1)
в результате получили горизонтальную асимптоту у = 0
теперь вертикальную
х = 1 точка разрыва
таким образом, точка х = 1 это точка разрыва II рода и
х=1 вертикальная асимптота.
2)
получили горизонтальную асимптоту у = 1
вертикальная
х= -3 точка разрыва
таким образом, точка х = -3 это точка разрыва II рода и
х= - 3 вертикальная асимптота.
MolkyWay:
Спасибо)))
пожалуйста. обращайтесь
Похожие вопросы
Предмет: Русский язык,
автор: osokinaalisa
Предмет: Математика,
автор: Алинчис1
Предмет: Математика,
автор: toshakovanadez
Предмет: Алгебра,
автор: MoeSimpson
Предмет: Математика,
автор: tanyaslem1