Предмет: Математика,
автор: MolkyWay
Ребята! Помогите! СРОЧНО!
Приложения:
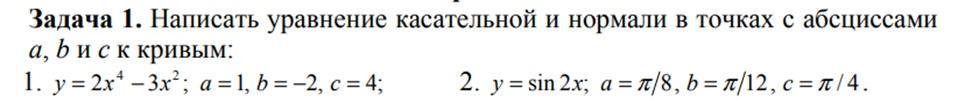
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
1) y= 2x⁴-3x²
уравнение касательной имеет вид
уравнение нормали имеет вид
y'(x) = 8x³-6x = -1
x₀ = 1
x₀ = -2
x₀ = 4
2) y=sin2x
x₀ = π/8
x₀ = π/12
x₀ = π/4
MolkyWay:
Очень вам благодарен)
не за что. обращайтесь -)). может, и запоздала с ответом, но вчера комп сдох, пришлось чинить. извините (((
Всё отлично)))
Похожие вопросы
Предмет: Другие предметы,
автор: annavaleriya6
Предмет: Английский язык,
автор: antonenko23735
Предмет: Физика,
автор: karetnikdarya2
Предмет: История,
автор: DGOTVK
Предмет: Литература,
автор: vololo14years