Question

ПОМОГИТЕ! много баллов
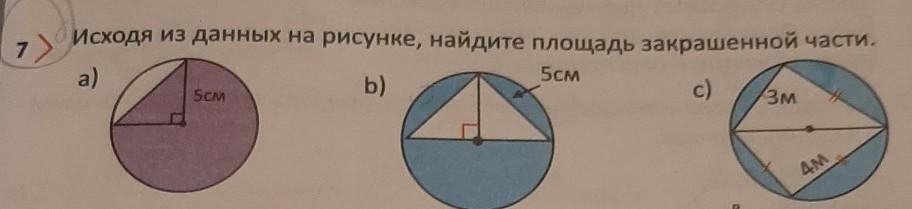
.Исходя из данных на рисунке, найдите площадь закрашенной части.
​

Answer 1

Ответ:

а) (75·π+50)/4 см²

b) (25·π-25)/2 см²

c) (25·π-48)/4 см²

Объяснение:

Нужно знать:

1) Площадь Sk круга радиуса R определяется по формуле: Sk=π·R².

2) Площадь Sт треугольника основанием a и высотой h определяется по формуле: Sт=a·h/2.

3) Вписанный угол равен половине угловой меры дуги, на которую он опирается.

Решение.

a) Поступим так: определим 3/4 часть площади круга и добавим площадь прямоугольного треугольника.

Площадь Sk круга радиуса 5 см равна:

Sk=π·5²=25·π см².

Теперь определим 3/4 часть площади круга Sч:

Sч=3·25·π/4=75·π/4 см².

Треугольник прямоугольный и один из катетов будет основанием, а другой высотой. Тогда:

Sт=5·5/2=25/2 см².

Площадь Sз закрашенной части равна:

Sз=Sч+Sт=75·π/4+25/2=(75·π+50)/4 см².

b) Так как один из углов треугольника опирается на дугу с угловой мерой 180°, то равен половине угловой меры этой дуги, то есть 90°. Значит, треугольник прямоугольный и равнобедренный.

Поэтому поступим так: определим площадь круга и отнимем площадь прямоугольного треугольника.

Диаметр d круга является гипотенузой равнобедренного прямоугольного треугольника с катетом 5 см. Применим теорему Пифагора:

d²=5²+5²=25+25=50 см².

Отсюда находим квадрат радиуса R круга:

R²=(d/2)²=d²/4=50/4=12,5 см².

Площадь Sk круга радиуса R равна:

Sk=π·R²=12,5·π см².

У прямоугольного треугольника один из катетов будет основанием, а другой высотой. Тогда:

Sт=5·5/2=25/2 см².

Площадь Sз закрашенной части равна:

Sз=Sк-Sт=12,5·π -25/2=(25·π-25)/2 см².

c) По рисунку видно, что стороны треугольников равны 3 см и 4 см. Угол треугольников, противолежащий к общей стороне опирается на дугу с угловой мерой 180°, то равен половине угловой меры этой дуги, то есть 90°. Значит, треугольники прямоугольные. Более того, равны.

Поэтому поступим так: определим площадь круга и отнимем площади прямоугольных треугольников.

Диаметр d круга является гипотенузой прямоугольного треугольника с катетами 3 см и 4 см. Применим теорему Пифагора:

d²=3²+4²=9+16=25 см².

Отсюда находим квадрат радиуса R круга:

R²=(d/2)²=d²/4=25/4 см².

Площадь Sk круга радиуса R равна:

Sk=π·R²=25·π/4 см².

У прямоугольного треугольника один из катетов будет основанием, а другой высотой. Тогда:

Sт=3·4/2=6 см².

Площадь Sз закрашенной части равна:

Sз=Sк-2·Sт=25·π/4 -2·6=25·π/4 -12=(25·π-48)/4 см².