Question

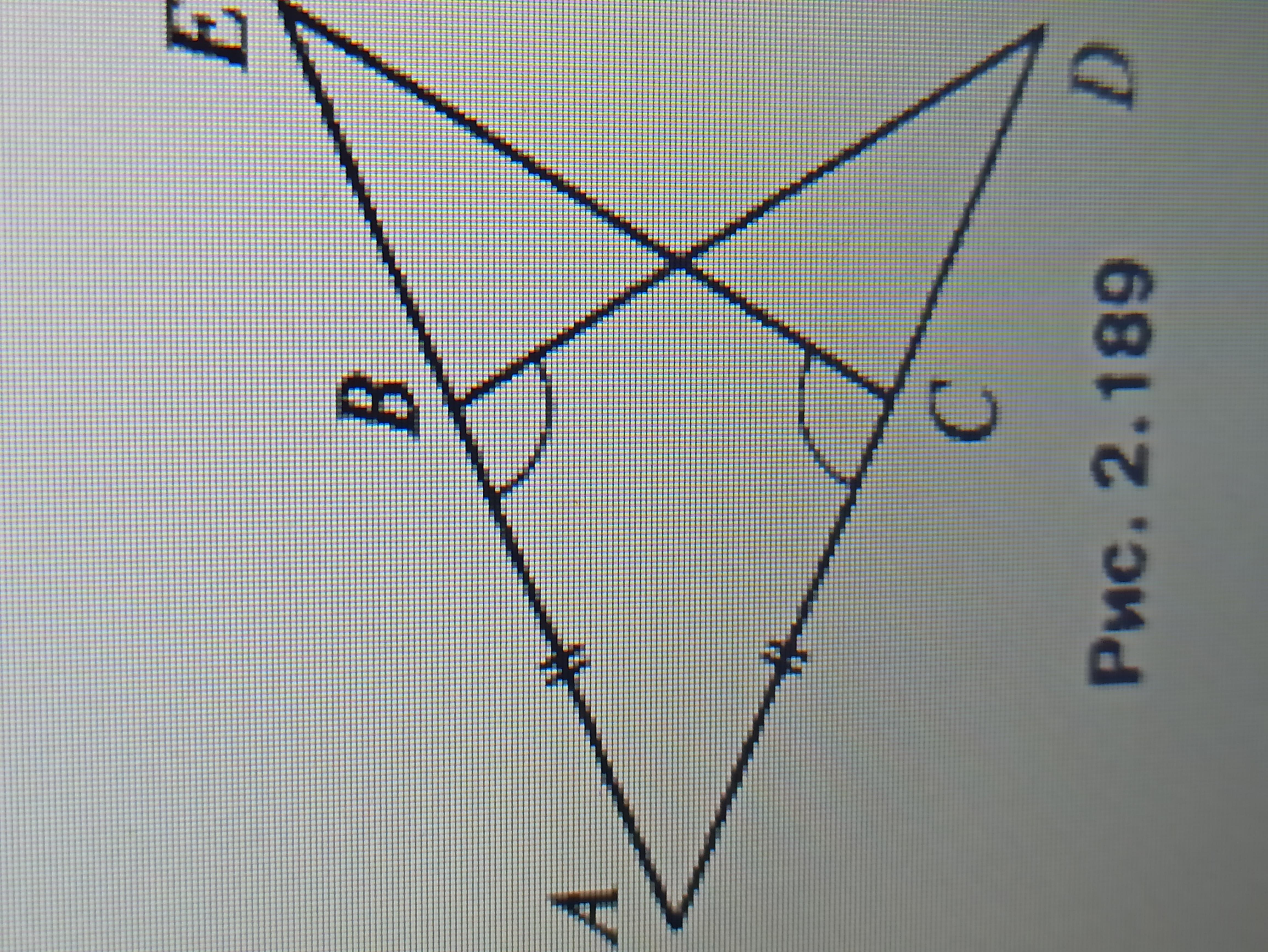
Дано: АЕ=15см ,ЕС=10см,АС=7см
Найти: периметр треугольника ВЕО, где О - точка пересечения СЕ и ВD

Answer 1

Ответ:

18 см

Объяснение:

Рассмотрим треугольники ABD и ACE:

• АВ = АС по условию,
• ∠ABD = ∠АСЕ по условию,
• ∠А - общий, значит

ΔABD = ΔACE по стороне и двум прилежащим к ней углам.

Из равенства треугольников следует, что

AD = AE = 15 см

BD = CE = 10 см

АВ = АС = 7 см

и ∠ADB = ∠AEC.

ВЕ = АЕ - АВ = 15 - 7 = 8 см

CD = AD - AC = 15 - 7 = 8 см, значит ВЕ = CD.

• ВЕ = CD,
• ∠ADB = ∠AEC,
• ∠ЕВО = ∠DCO как углы, смежные с равными углами,

значит, ΔВЕО = ΔCOD по стороне и двум прилежащим к ней углам.

Сумма периметров этих треугольников:

$P_{BOE}+P_{COD}=BE+CD+BD+CE=8+8+10+10=36$ см

Так как треугольники равны, то равны их периметры, тогда

$P_{BOE}=36:2=18$ см