Предмет: Геометрия,
автор: Maps1OF
В трапеции основания равны 40 и 90, а боковые стороны равны 40 и 30.
Найдите высоту трапеции. даю 15 балов за быстрый ответ
Ответы
Автор ответа:
3
Ответ:
24 ед.
Объяснение:
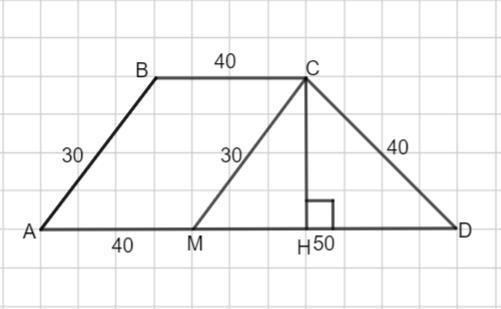
Пусть дана трапеция ABCD.
Боковые стороны AB=30 ед., CD=40 ед.
Основания AD=90 ед., BC=40 ед.
Проведем СМ║ АВ
Тогда АВСМ - параллелограмм ( противолежащие стороны попарно параллельны.
Значит, АВ=СМ= 30 ед., ВС= АМ= 40 ед.
МD=AD-AM=90-40= 50 ед.
Рассмотрим треугольник MCD.
По теореме, обратной теореме Пифагора, треугольник MCD - прямоугольный, так как
Высота этого прямоугольного треугольника MCD является высотой трапеции.
Найдем высоту прямоугольного треугольника. Для этого произведение катетов надо разделить на гипотенузу.
Значит, высота трапеции равна 24 ед.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: alenkii88
Предмет: Русский язык,
автор: nat2015
Предмет: География,
автор: kaneussden
Предмет: Алгебра,
автор: привет052
Предмет: История,
автор: Ychenik010203