Предмет: Математика,
автор: lovenesS
Найти производные dy/dx данных функций
Приложения:
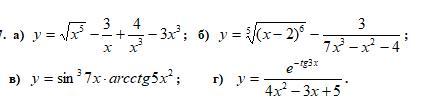
Ответы
Автор ответа:
1
а)
б)
в)
г)
88653:
здравствуйте зайдите на мой вопрос алгебра люди
Похожие вопросы
Предмет: История,
автор: anna513
Предмет: Русский язык,
автор: Pr200000
Предмет: Математика,
автор: allapugacheva
Предмет: Алгебра,
автор: sivikivi5