Question

Сопоставьте коэффициенты в уравнении ax3+bx2+cx+d=0 с их значениями, если известно, что его корнями являются 1,(−1±3)/2 .

Answer 1

Ответ:

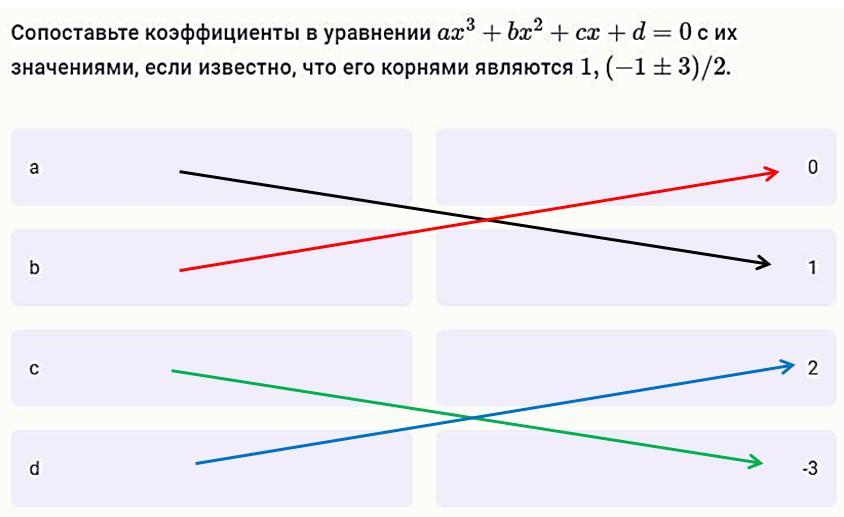
a = 1, b = 0, c = -3, d = 2

Объяснение:

Дано кубическое уравнение

a·x³+b·x²+c·x+d=0

с корнями 1, (-1±3)/2.

Отсюда корни уравнения

x₁ = 1, x₂ = 1, x₃ = -2.

Применим теорему Виета для кубического уравнения:

Если x₁, x₂ и x₃ корни кубического уравнения a·x³+b·x²+c·x+d=0, то

$\tt x_1+x_2+x_3=-\dfrac{b}{a}, \\\\ x_1 \cdot x_2+x_1 \cdot x_3 + x_2 \cdot x_3=\dfrac{c}{a},\\\\x_1 \cdot x_2 \cdot x_3 = -\dfrac{d}{a}.$

Так как корни известны, то

$\tt -\dfrac{b}{a}=1+1-2=0 \Rightarrow b=0 , \\\\ \dfrac{c}{a}=1 \cdot 1+1 \cdot (-2) + 1 \cdot (-2)=-3 \Rightarrow c= -3 \cdot a ,\\\\-\dfrac{d}{a}=1 \cdot 1 \cdot (-2) = -2 \Rightarrow d= 2 \cdot a.$

Получаем следующий вид кубического уравнения:

a·x³-3·a·x+2·a=0

или так как a≠0:

x³-3·x+2=0.

Отсюда находим коэффициенты:

a = 1, b = 0, c = -3, d = 2.