Предмет: Математика,
автор: Kolyanka97
нужно решить под цифрой 4 и 5
Приложения:
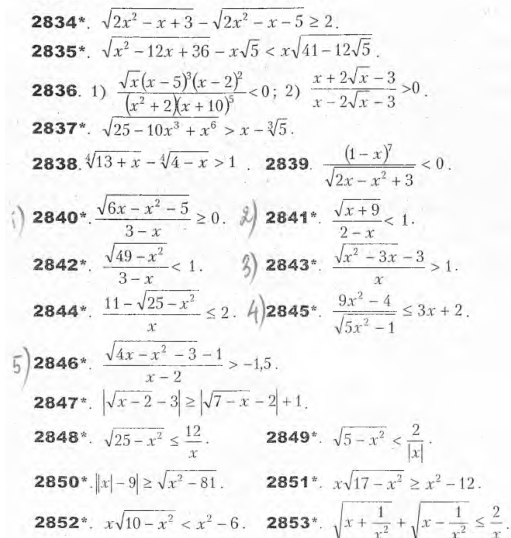
Ответы
Автор ответа:
0
Объединяем получаем
объединяем получаем
Похожие вопросы
Предмет: Физкультура и спорт,
автор: Аноним
Предмет: Биология,
автор: dianamirnaya68
Предмет: Английский язык,
автор: babaevaradina86
Предмет: Алгебра,
автор: zzzzzzz0707
Предмет: Геометрия,
автор: maloq