Предмет: Геометрия,
автор: Andrey5634
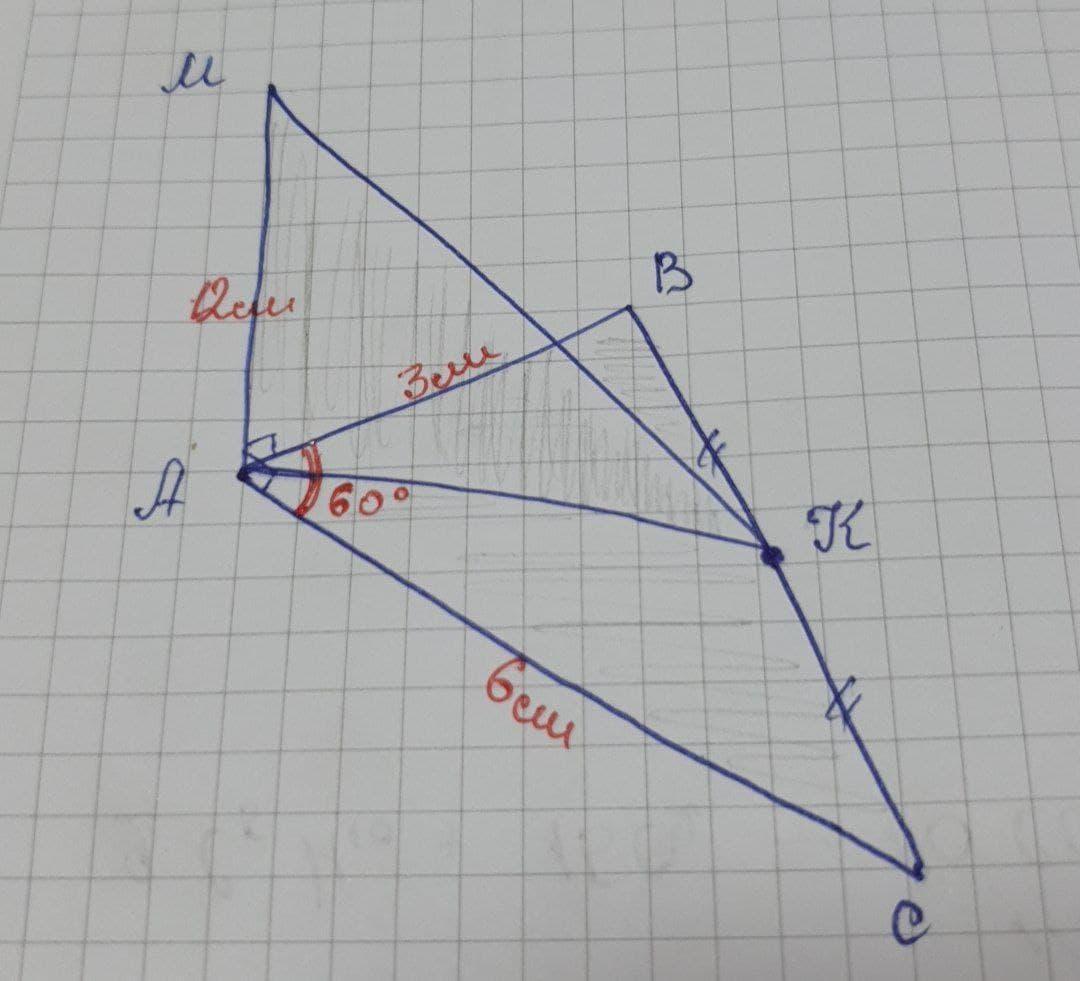
В треугольнике АВС угол между сторонами АВ = 3 см и АС = 6 см равен 60°.
В вершине этого угла построен перпендикуляр АМ = 12 см к плоскости
треугольника. Найдите расстояния от концов перпендикуляра к середине
стороны ВС.
Ответы
Автор ответа:
2
Ответ:
АК=
МК=
Объяснение:
Надо найти АК и МК
Пусть К - середина стороны ВС.
По теореме косинусов:
ВС²=АВ²+АС²-2*АВ*АС*cos∠A = 9+36-2*3*6* = 27
ВС=√27,
ВК=КС= √27/2
Применим обратную т.Пифагора к ΔАВС:
АВ²+ВС²=АС² - проверим равенство. Если оно истинное, значит ∠В=90°
3²+(√27)² = 6²
9+27=36
36=36 - равенство верное, ⇒∠В=90° , ΔАВС - прямоугольный
Рассмотрим ΔАВК (∠В=90°).
По теореме Пифагора: АК²= АВ²+ВК² = 9+ 27/4 = 63/4
АК= - нашли первое расстояние.
Рассмотрим ΔАМК.
Т.к. АМ⊥(АВС), то АМ перпендикулярна любой прямой в этой плоскости, а значит АМ⊥АК. ΔАМК - прямоугольный. ∠А=90°
По теореме Пифагора: МК²=АМ²+АК²=144+63/4=639/4
МК= - нашли второе расстояние
Приложения:
Похожие вопросы
Предмет: География,
автор: margaritalitvin
Предмет: Химия,
автор: MTZ
Предмет: Алгебра,
автор: quliav3812
Предмет: Математика,
автор: Zores