Question

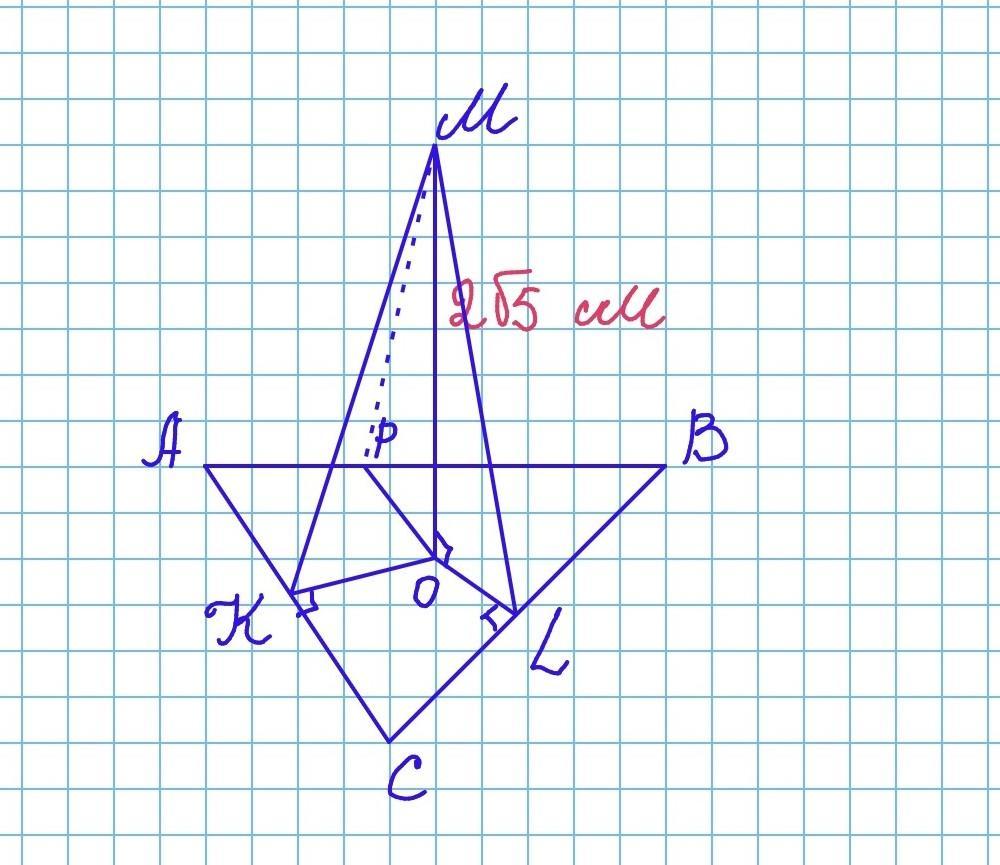
У трикутнику АВС вписано коло із центром О. Через точку О проведено пряму МО, перпендикулярну до площини АВС. Точка М віддалена від цієї площини на 2 корфнь з 5 см. Знайдіть відстань від точки М до сторін трикуника, якщо АВ=13 см, ВС=14 см, АС=15 см

Answer 1

Ответ:

6 см

Пошаговое объяснение:

Якщо коло, с центром у  точці О вписане в трикутник АВС (точки  L,K,P - точки дотику кола до сторін ВС, АС і АВ  відповідно), то OL, OK,OP - радіуси вписаного кола ( OL ⟂ BC, OK ⟂ AC, OP ⟂AB) i відстані від центра кола до сторін трикутника АВС.

• Площа трикутника дорівнює добутку півпериметра трикутника на радіус вписаного кола.

S=r×p,

p- півпериметр трикутника,

$p = \dfrac{a + b + c}{2} = \dfrac{13 + 14 + 15}{2} = 21$

r - радіус вписаного кола.

=> r= S/p

Площу трикутника знайдемо по формулі Герона:

$s = \sqrt{p(p- a)(p - b)(p - c)} = \sqrt{21(21 - 13)(21 - 14)(21 - 15)} = \\ = \sqrt{3 \times 7 \times 8 \times 7 \times 6} = 7 \times 12 = 84$

$r = \dfrac{s}{p} = \dfrac{84}{21} = 4$ см

Трикутники MOL, MOK, MOP рівні за двома катетами.

=> Відстань від точки М до сторін трикутника (ML=MK=MP) знайдемо по т.Піфагора:

ML=

$= \sqrt{ {OM}^{2} + {OL}^{2} } = \sqrt{( {2 \sqrt{5)} }^{2} + {4}^{2} } = \sqrt{20 + 16} = 6$ см