Предмет: Геометрия,
автор: kenusaoskelen
Из точки к плоскости прямоугольного треугольника с катетами 15 и 20 см проведен перпендикуляр длиной 16 см. Основание перпендикуляра, вершина прямого угла треугольника. Найдите расстояние от данной точки до гипотенузы.
Ответы
Автор ответа:
29
Ответ:
SD=20см
Найти расстояние от данной
точки до гипотенузы.
Объяснение:
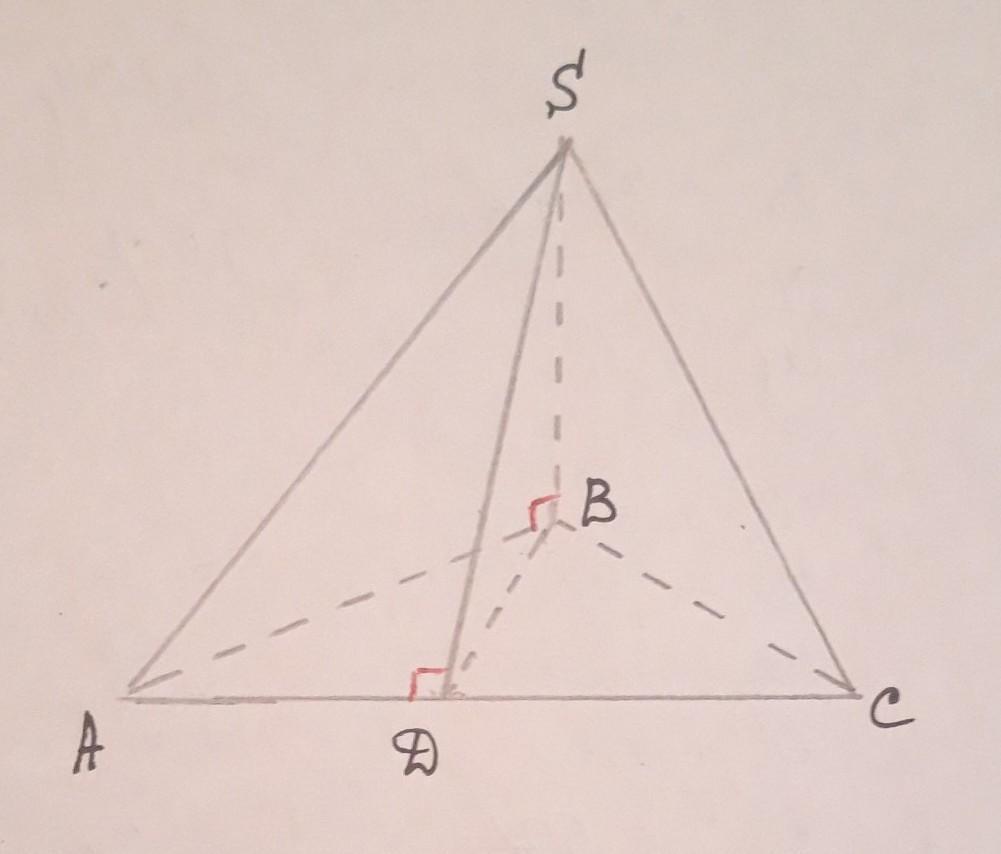
Дано:
треуг. АВС
<АВС=90°
SB перпендик. плос. АВС
SB=16см
АВ=15см
ВС=20см
SD перпендик. АВ
-----------------------------------------
SD - ?
Рассмотрим треуг.АВС.
По теореме Пифагора:
АС^2=АВ^2+ВС^2
АС=
Из треуг. АВС:
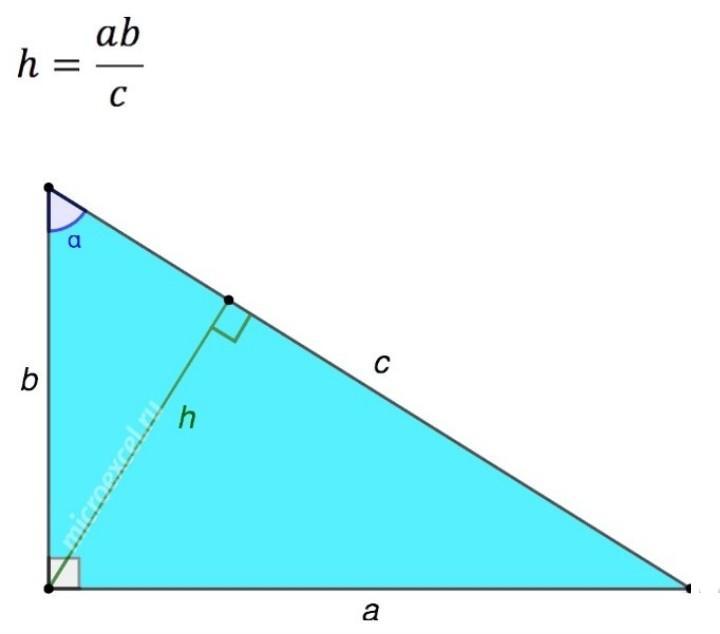
DB=AB×BC/AC=
Рассмотрим треуг. SBD.
Он по условию прямоугольный
с катетами SB и ВD, a SD - его
гипотенуза.
По теореме Пифагора:
SD^2=SB^2+BD^2
SD=
Ответ:
SD=20см
Приложения:

badimork:
а что за SD?
когда его на рисунке показать
где*
там есть картинка, полистайте.
да она есть
но там нету многих данных
спасибо вам за ответ
вы очень помогли
а с SD я уже разобрался
Похожие вопросы
Предмет: Английский язык,
автор: Настя4571
Предмет: Химия,
автор: мертвыйхудожник
Предмет: Математика,
автор: radosteva02
Предмет: Литература,
автор: fanhi6