Предмет: Алгебра,
автор: LюКа
Решите, пожалуйста, уравнения, подробно расписав ход вычислений.
Приложения:
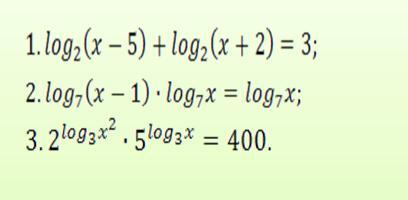
Ответы
Автор ответа:
12
Ответ:
1. log2(x-5)+log2(x+2)=3
ОДЗ : х принадлежит (5;+∞]
log2((x-5)*(x+2))=3
log2(x²+2x-5x-10)=3
x²+2x-5x-10=2³
x²-3x-10=8
x²-3x-10-8=0
x²+3x-6x-18=0
x(x+3)-6(x+3)=0
(x-3)(x-6)=0
1)x+3=0 ; x= -3
2)x-6=0 ; x=6, но с учётом ОДЗ :
х=6.
2. log7(x-1)*log7(x)=log7(x)
ОДЗ : x принадлежит (1;+∞]
log7(x-1)*log7(x)-log7(x)=0
log7(x)*(log7(x-1)-1)=0
1)log7(x)=0 ; x=1 ; 2) log7(x-1)=0 ; log7(x-1)=1 ; x-1=7 ; x=7+1 ; x=8, но с учётом ОДЗ : х=8.
Объяснение:
3. 2^log3(x²). *5^log3(x). = 400.
ОДЗ : х принадлежит (0;+∞]
2^2log3(|x|). * 5^log3(x). = 20²
2^2log3(x). * 5^log3(x)=20²
4^log3(x). * 5^log3(x). = 20²
(4*5)^log3(x). = 20²
20^log3(x). = 20²
log3(x)=2
x=3²
x=9
Похожие вопросы
Предмет: Математика,
автор: ундалов
Предмет: Химия,
автор: Viktor132
Предмет: Химия,
автор: saba2000kub
Предмет: Математика,
автор: MariyKot
Предмет: Литература,
автор: dvolzhenkov