Предмет: Алгебра,
автор: pavchenskaya
70 баллов
Помогите пожалуйста
Приложения:
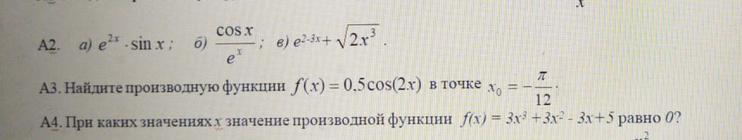
pavchenskaya:
Пожалуйста с точным решением
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Математика,
автор: maksimfadeevp
Предмет: Химия,
автор: james5f5
Предмет: Математика,
автор: nataskasuponki
Предмет: Биология,
автор: Natutp113
Предмет: История,
автор: njvbyf04Юля