Предмет: Математика,
автор: yommany
Помогите решить методом Гаусса срочно ( не пишите тип фото размытое и тд )
Приложения:
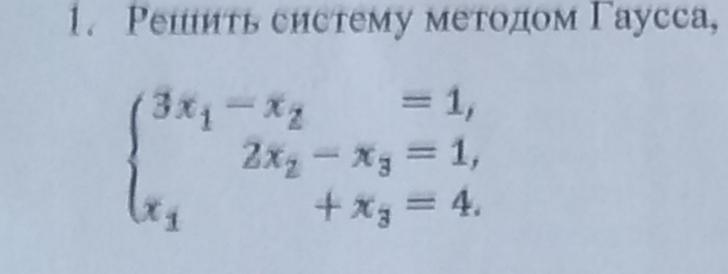
Ответы
Автор ответа:
1
Ответ:
х1=1;х2=2;х3=3
Пошаговое объяснение:
Матричный вид записи: Ax=b, где
- А=
b = 1;1;4 (Сверху вниз, в один столбец)
- Далее строим расширенную матрицу ( Также, только значения б добавляем справа под квадратную скобку)
- Обозначим через aij элементы i-ой строки и j-ого столбца. Первый этап. Прямой ход Гаусса.
- Исключим элементы 1-го столбца матрицы ниже элемента a1,1. Для этого сложим строку 3 со строкой 1, умноженной на -1/3:
b = 1; 1; 11/3 (также сверху вниз, в один столбец)
- Исключим элементы 2-го столбца матрицы ниже элемента a2,2. Для этого сложим строку 3 со строкой 2, умноженной на -1/6: получим (буду писать текстом, так быстрей) 1 строка = 3;-1;0, 2 строка 0;2;-1, 3 строка 0;0;7/6. b = 1;1;7/2
- Делим каждую строку матрицы на соответствующий ведущий элемент, получаем: 1 строка = 1;-1/3;0, 2 строка = 0;1;-1/2, 3 строка = 0;0;1. b = 1/3;1/2/3
- Из расширенной матрицы восстановим систему линейных уравнений, Базисные переменные x1, x2, x3. и получаем: x1=1/3+1/3(х2);х2=1/2+1/2(х3);х3=3
- Подставив нижние выражения в верхние, получим решение: х1=1;х2=2;х3=3
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: TRUSOV06
Предмет: Геометрия,
автор: alexb2000
Предмет: Биология,
автор: 87009522377
Предмет: Математика,
автор: карина2116