Question

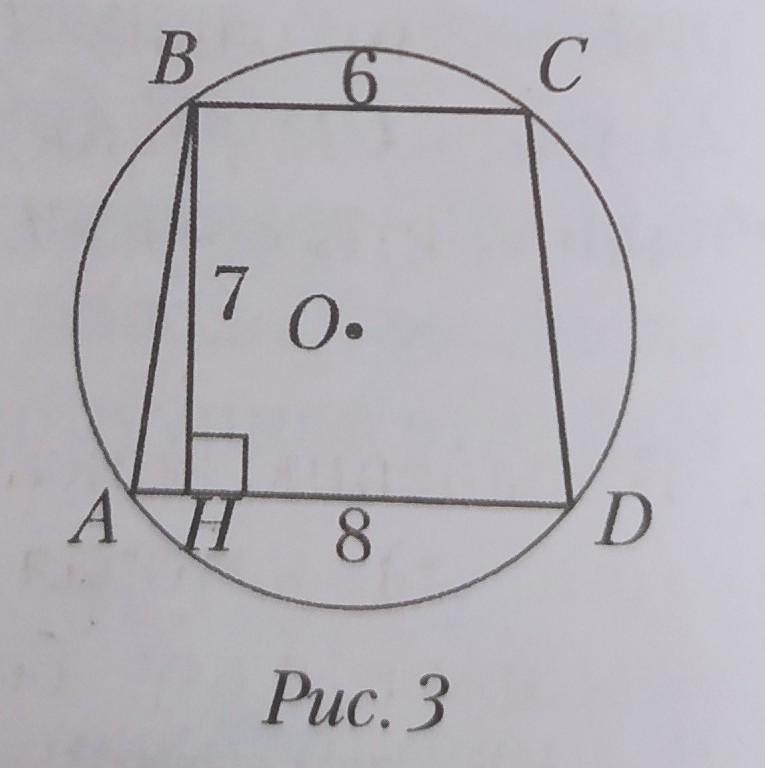
Трапеция ABCD вписана в окружность (рис. 3). Основания ВС и AD трапеции равны 6 см и 8 см, высота ВН равна 7 см. Найдите длину стороны CD.​

Answer 1

Ответ:

СD = 5√2 ед.

Объяснение:

Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Следовательно, вписанная в окружность трапеция АВСD равнобедренная.

В равнобедренной трапеции высота ВН (смотри рисунок в приложении к условию) делит основание АD трапеции на два отрезка, меньший из которых (АН) равен полуразности двух оснований (свойство).

Итак, в прямоугольном треугольнике АВН катет АН = (8 - 6)/2 =1.

Второй катет ВН = 7 (дано).

По Пифагору гипотенуза АВ = √(АН² + ВН²) = √(1+49) = √50 = 5√2 ед.

Так как боковые стороны равны, то ответ:

CD = 5√2 ед.