Предмет: Геометрия,
автор: vikasveta1219
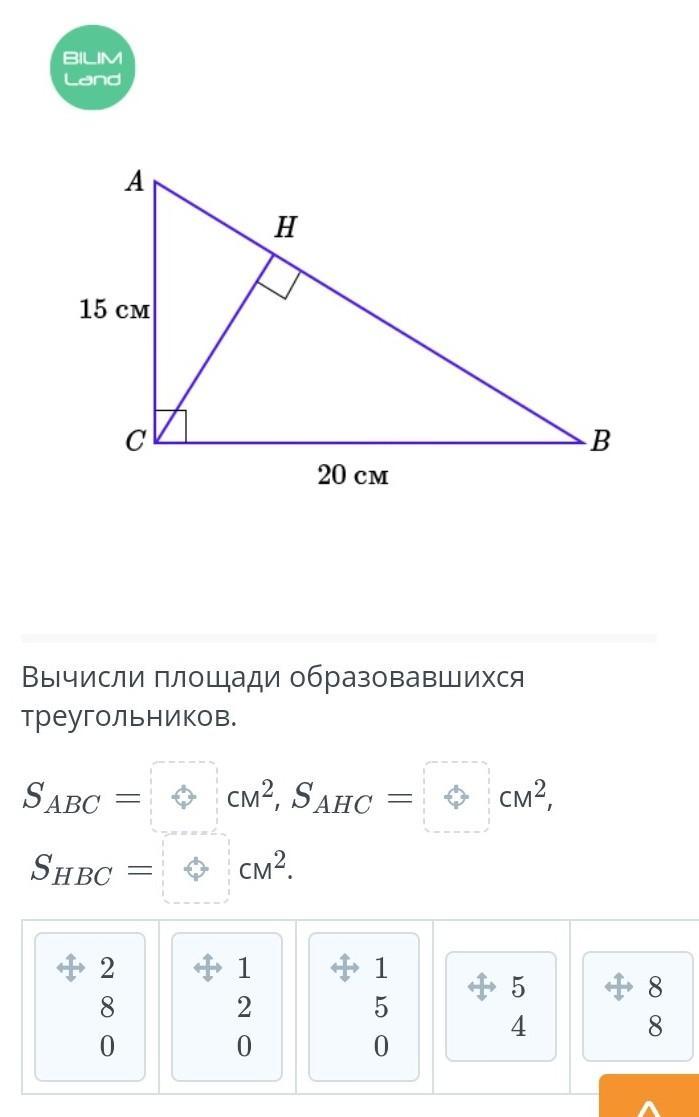
Через вершины прямого угла прямоугольного треугольника с катетами 15 см и 20 см проведен перпендикуляр к гипотенузе. Вычисли площадь образовавшихся треугольников.
Приложения:
Ответы
Автор ответа:
1
Ответ:
S abc = 150 см²
S ahc = 54 см²
S bhc = 96 см²
Объяснение:
- Т. к. ∆ - прямоугольный (п/у) => формула площади:
- С помощью теоремы Пифагора найдём гипотенузу:
- С помощью S∆ найдём высоту CH:
- С помощью теоремы Пифагора найдём АН в п/у ∆АНС
- Тогда S ∆AHC:
- Тогда S ∆BCH будет равна разности S ∆ABC и S ∆AHC ( по свойству площадей )
Похожие вопросы
Предмет: Алгебра,
автор: Sasha130197
Предмет: Математика,
автор: krasota100suh
Предмет: Литература,
автор: YurOKOrsK
Предмет: Информатика,
автор: gc12
Предмет: Математика,
автор: maiorov27