Question

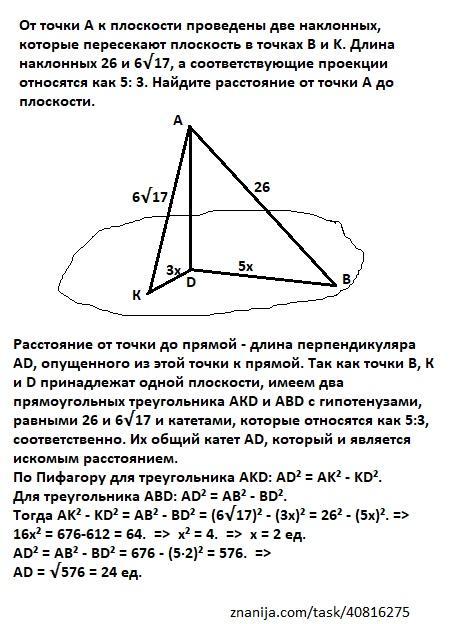
От точки A к плоскости проводят два откоса, которые пересекают плоскость в точках B и K. Длина расхождений 26 и 6 корень из 17, а пропорции соответствующих выступов 5: 3. Нарисуйте диаграмму по условию расчета и найдите расстояние от точки А до плоскости.

Answer 1

Ответ:

Расстояние от точки А до плоскости равно 24 ед.

Объяснение:

Расстояние от точки до прямой - длина перпендикуляра АD, опущенного из этой точки к прямой. Так как точки В, К и D принадлежат одной плоскости, имеем два прямоугольных треугольника АКD и ABD с гипотенузами, равными 26 и 6√17 и катетами, которые относятся как 5:3, соответственно. Их общий катет AD, который и является искомым расстоянием.

По Пифагору для треугольника AKD: AD² = AK² - KD².

Для треугольника AВD: AD² = AВ² - ВD².

Тогда AK² - KD² = AВ² - ВD² = (6√17)² - (3х)² = 26² - (5х)². =>

16х² = 676-612 = 64.  =>  x² = 4.  =>  х = 2 ед.

AD² = АВ² - BD² = 676 - (5·2)² = 576.  =>

AD = √576 = 24 ед.