Question

Даю 70 баллов :) иу​

Answer 1

Ответ:

1) случай

Боковая сторона - $\frac{58}{3}$

Основание - $\frac{79}{3}$

2)случай

Боковая сторона - 24

Основание - 17

Объяснение:

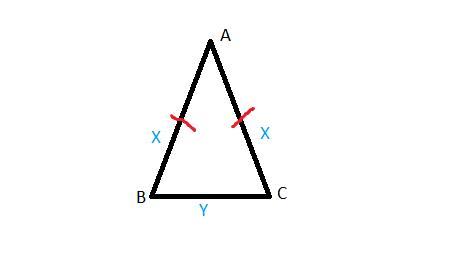
Пусть боковые стороны треугольника равны x, а основание y.

По условию y = x + 7 или x = y + 7 по условию неизвестно что больше основание  или боковая сторона ;Периметр треугольника это сумма его сторон.

1) случай y = x + 7;

y + x + x = 65

y + 2x = 65

x + 7 + 2x = 65

3x = 58

x = $\frac{58}{3}$

y = x + 7 = $\frac{58}{3} + 7$ = $\frac{79}{3}$

Проверим неравенство треугольника:

AB + AC > BC

$\frac{58}{3} +\frac{58}{3} >\frac{79}{3} \\\frac{116}{3} >\frac{79}{3}$

Следовательно неравенство верно и треугольник существует

2) cлучай

x = y + 7;

y + x + x = 65

y + y + 7 + y + 7 = 65

3y + 14 = 65

3y = 51

y = 17

x = y + 7 = 17 + 7 = 24

Проверим неравенство треугольника:

AB + AC > BC

24 + 24 > 17

28 > 17

Следовательно неравенство верно и треугольник существует