Question

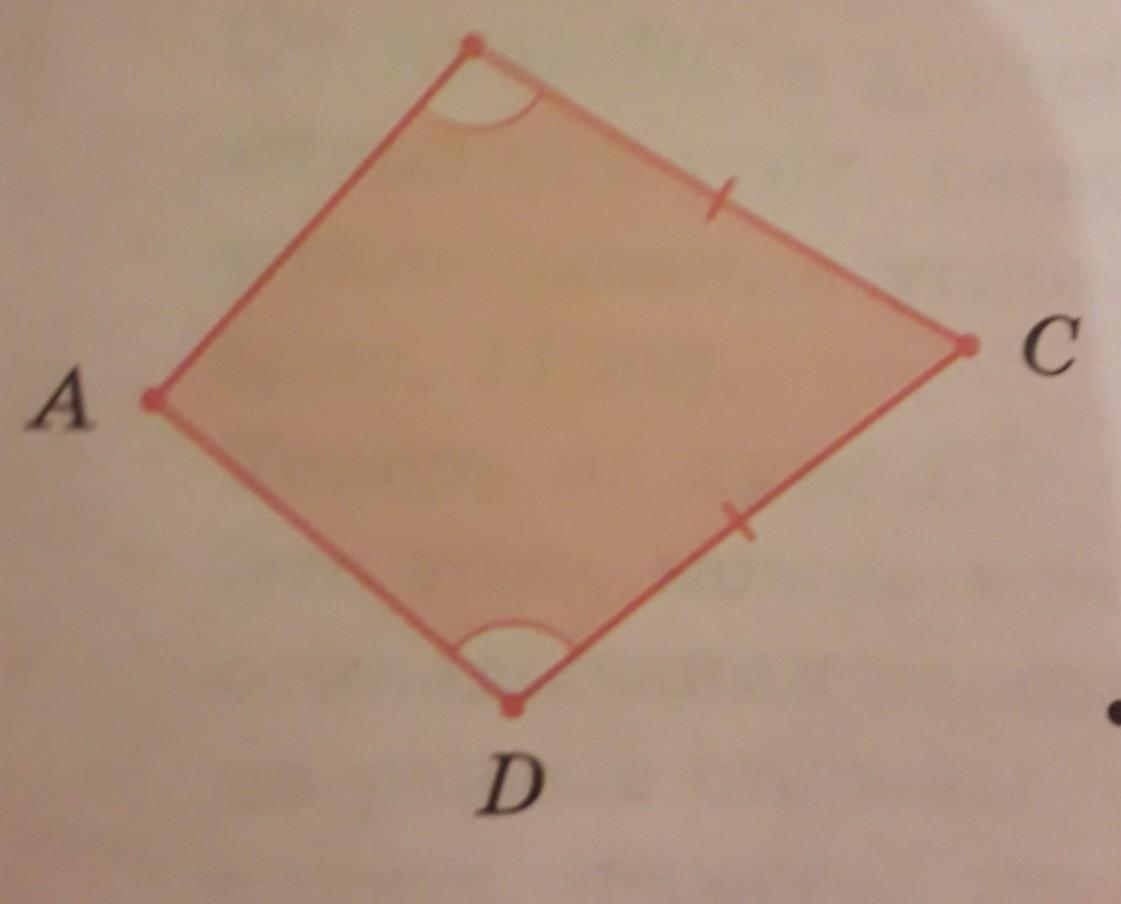
В четырёхугольнике ABCD угол ABC равен углу ADC,BC=CD.Докажите, что его диагонали перпендикулярны друг другу .​

Answer 1

Ответ:

Доказано: AC⊥BD

Объяснение:

Дано:

ABCD - четырехугольник.

∠B=∠D

BC=CD

___________________________

Доказать: AC⊥BD

Доказательство:

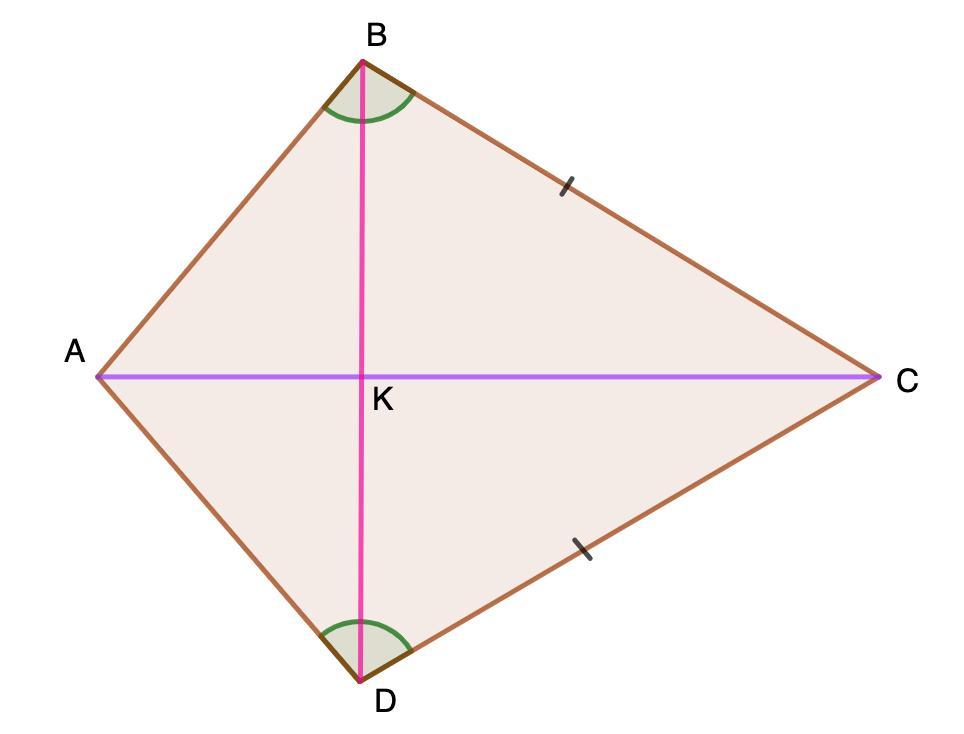
Проведем диагонали AC и BD.

1. Рассмотрим ΔABC и ΔACD.

BC=DC (по условию)

AC - общая

∠B=∠D (по условию)

⇒ ΔABC = ΔACD (по 1 признаку)

⇒ ∠BCA=∠ACD (как соответственные элементы);

2. Рассмотрим ΔBCD - равнобедренный (BC=CD)

∠BCA=∠ACD (п.1)

⇒ CK - биссектриса (п.2), высота (свойство равнобедренного Δ-ка)

⇒ AC⊥BD