Question

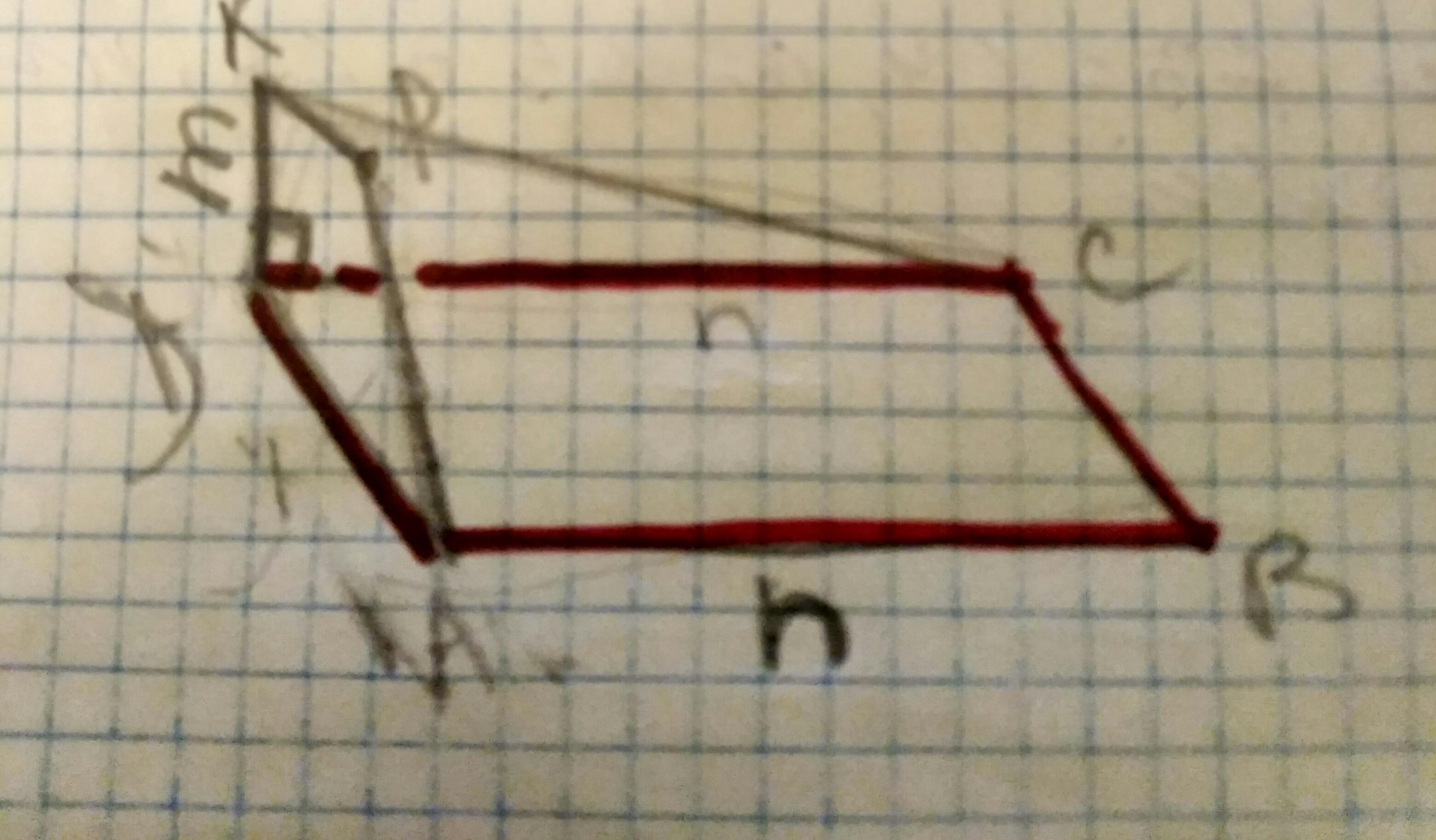
Известно, что плоскости a и b взаимно перпендикулярны, ABCD
- параллелограмм в плоскости a, ADKP - трапеция в плоскости b.
Определите, существует ли плоскость, в которой лежат прямые:
а) BC и PK; б) DC и AP; в) DC и DK. Найдите величину угла CDK. Найдите
длину KC, считая KD=m, AB =n

Полное решение, можно без дано.

Answer 1

Ответ:

1) Да существует

РК║АD( основания параллелограмма), и BC║AD (стороны параллелограмма), значит РК║ВС и есть такая плоскость в которой лежат эти прямые

2)НЕт, не существует  , так как  DC и AP -это скрещивающиеся прямые нет общей точки

3)Да, существует . Есть общая точка - это пересекающиеся прямые.

Величина ∠CDK=90°, так по условию α⊥β, CD ∈ β , а DK ∈ α, отсюда

DK⊥CD.

По т. Пифагора  KC= DК²+CD ². CD= АВ=m( так как ABCD

- параллелограмм, а у него противоположные стороны равны)

$KC=\sqrt{m^2+n^2}$