Предмет: Алгебра,
автор: aygerymtacion17
найти решение неопределённых интегралов
Приложения:
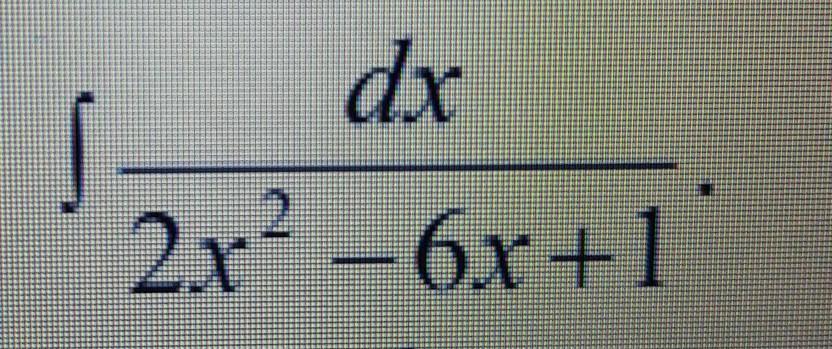
Ответы
Автор ответа:
1
Ответ:
Выделяем квадрат в знаменателе:
Похожие вопросы
Предмет: Математика,
автор: irinaceb
Предмет: Английский язык,
автор: pmagamaeva
Предмет: Русский язык,
автор: fainasultanova
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Ilyauhdhbtxskr