Предмет: Алгебра,
автор: klkifl
3.В геометрической прогрессии b3=1/3,b4=1/6. Найдите b5. Найдите сумму пяти первых членов этой прогрессии.
Приложения:
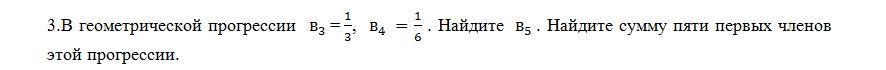
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Биология,
автор: coolirina2404
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: dmonares
Предмет: Литература,
автор: лолитафриз