Предмет: Геометрия, автор: soand

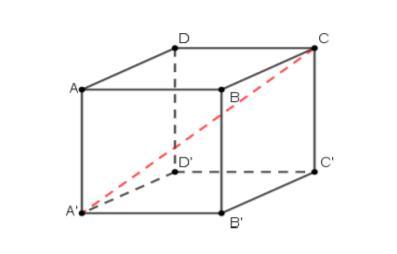
ABCDA'B'C D' в единичном кубе. Найдите косинус угла между плоскостью ABCD и прямой AСˊ

Приложения:

Ответы

Автор ответа: Andr1806

Ответ:

cos(A'CA) = √6/3.

Объяснение:

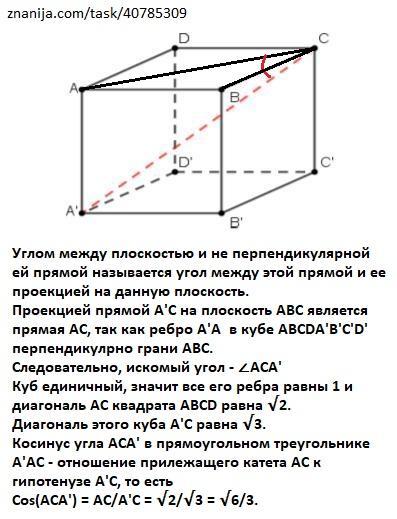
Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.

Проекцией прямой А'С (диагональ куба) на плоскость АВСD является прямая АС (диагональ грани АВСD), так как ребро АА' куба АВСDA'B'C'D' перпендикулярно грани АВСD.

Следовательно, искомый угол - ∠ACA'.

Куб единичный, значит все его ребра равны 1 и диагональ АС = √2, а диагональ куба A'C = √3.

Косинус угла АСA' в прямоугольном треугольнике А'АС - отношение прилежащего катета АС к гипотенузе А'С, то есть

Cos(ACA') = AC/A'C = √2/√3 = √6/3.

Приложения: