Предмет: Геометрия,
автор: fireyutuber98
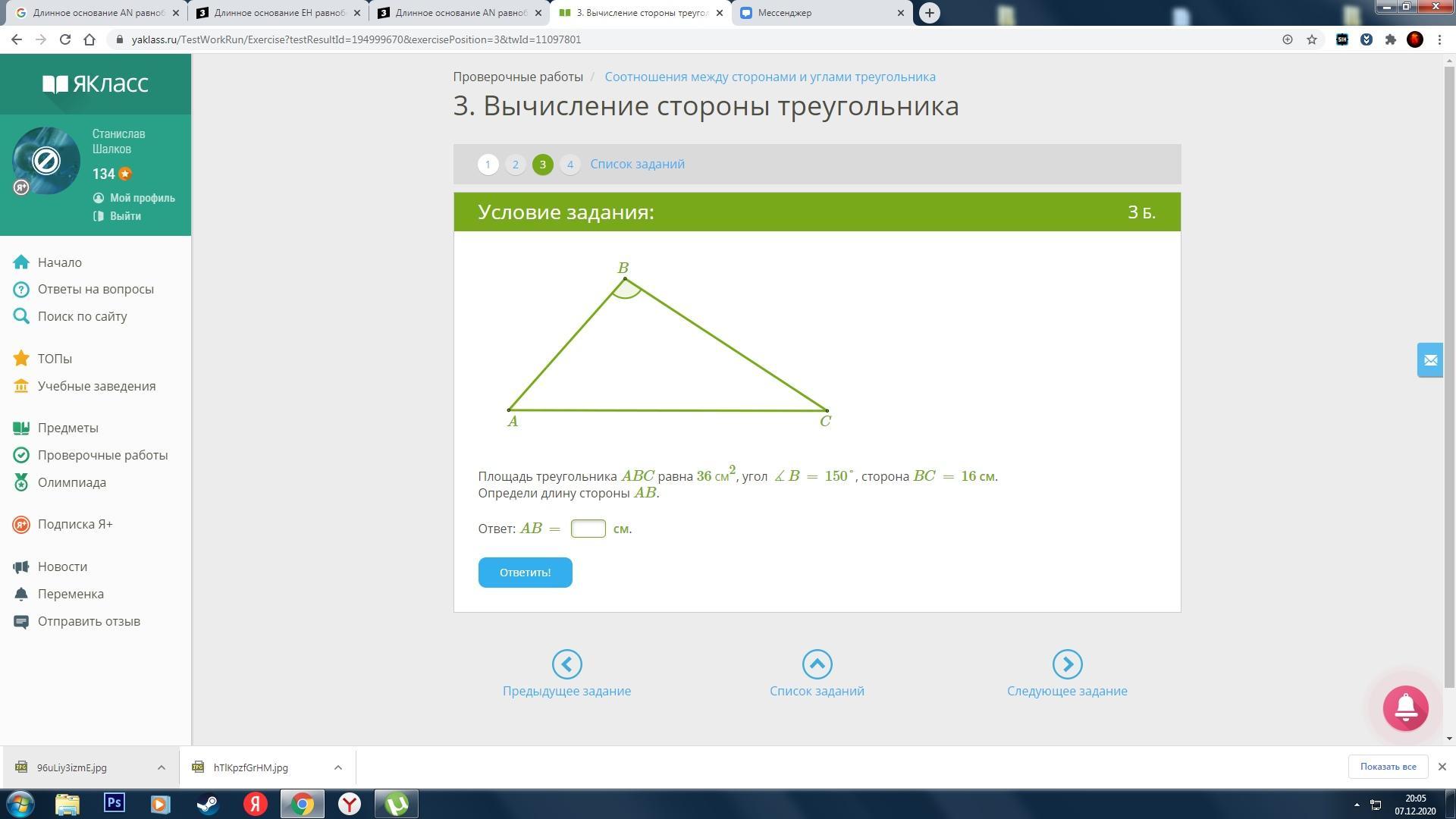
Площадь треугольника ABC равна 36 см2, угол ∡B=150°, сторона BC=16 см.
Определи длину стороны AB.
Приложения:
Ответы
Автор ответа:
4
Площадь треугольника можно вычислить как полупроизведение двух сторон на синус угла между ними:
Для треугольника АВС:
150° - тупой угол, синус тупого угла:
Уравнение по формуле площади треугольника:
Ответ: AB = 9 см.
Похожие вопросы
Предмет: Русский язык,
автор: cacha2005
Предмет: Английский язык,
автор: Polya9
Предмет: Математика,
автор: фюн
Предмет: Литература,
автор: deadpool2478