Предмет: Алгебра,
автор: t993876321
Пожалуйста помогите мне с решением Срочно нужно.
Приложения:
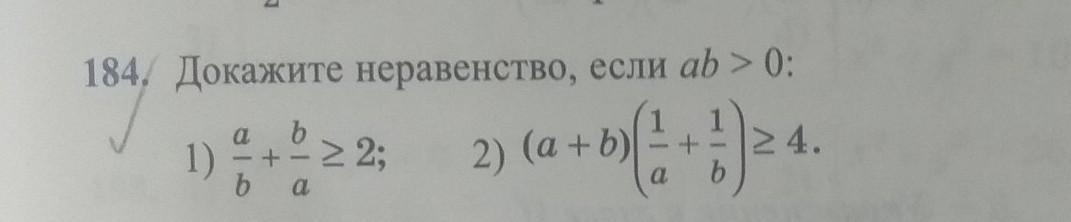
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Так как (a-b)²≥0 и ab>0 ⇒
Так как (a-b)²≥0 и ab>0 ⇒
Похожие вопросы
Предмет: Математика,
автор: fhjutedfhjjjgff
Предмет: География,
автор: Vance96
Предмет: Математика,
автор: Дарья459
Предмет: Обществознание,
автор: kjk123ggt
Предмет: МХК,
автор: arishaprohorenk