Предмет: Геометрия,
автор: tatos75
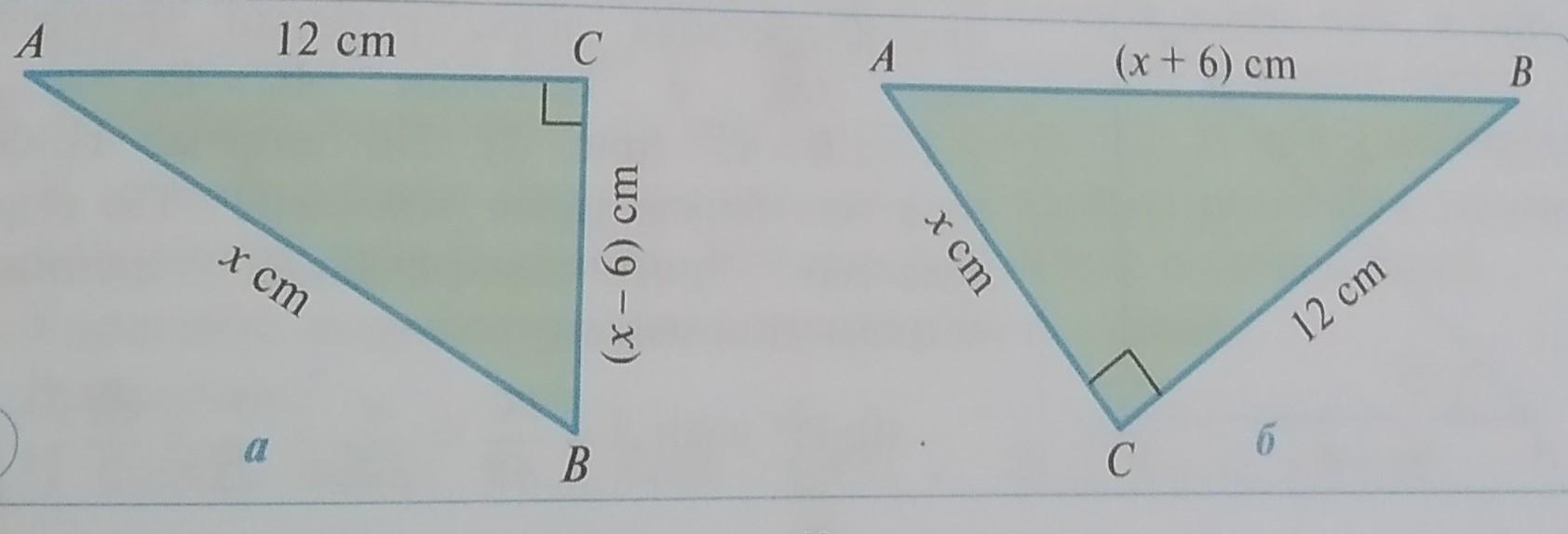
Найдите неизвестные длины (рис. 2), и вычислите синус, косинус,
тангенс и котангенс острых углов.
Приложения:
Ответы
Автор ответа:
28
Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе.
Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе.
Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).
Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему).
Первый рисунок
По теореме Пифагора найдём стороны треугольника.
АС²+ВС²=АВ²
12²+(х-6)²=х²
144+х²-12х+36=х²
12х=180
х=15
Гипотенуза АВ=15 см
Катет ВС = 15-6 = 9 см
Катет АС = 12 cм - по условию
Второй рисунок
По теореме Пифагора найдём стороны треугольника.
АС²+ВС²=АВ²
х² + 12²=(х+6)²
х²+144 = х²+12х+36
12х=108
х=9
Катет АС = 9 см
Катет ВС = 12 см по условию
Гипотенуза АВ=9+6 = 15 см
Похожие вопросы
Предмет: Обществознание,
автор: aruzhan240304
Предмет: Українська мова,
автор: midyanyivalenti
Предмет: Русский язык,
автор: Р3е5г8и2н1а
Предмет: Информатика,
автор: ыкьныкеь