Предмет: Алгебра,
автор: ata221
СРОЧНО!!! ДВА НЕРАВЕНСТВА!
Показать в единичной окружности и указать направление
Приложения:

Ответы
Автор ответа:
1
Ответ:
Приложения:
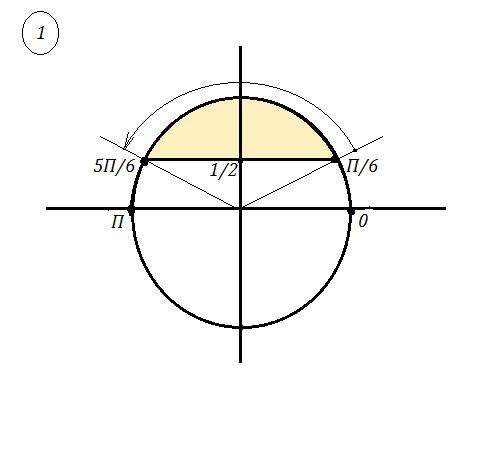
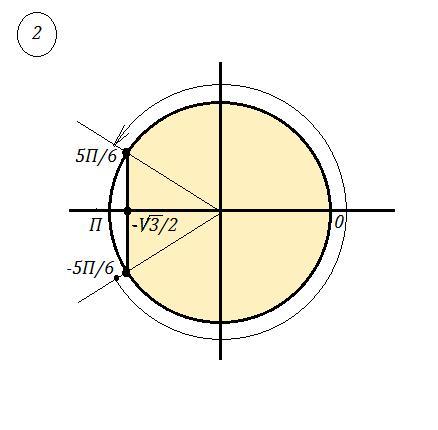
ata221:
можете помочь, пожалуйста, с решением неравенства?
Похожие вопросы
Предмет: Алгебра,
автор: Proof57
Предмет: Математика,
автор: missisLizushka
Предмет: Литература,
автор: Аноним
Предмет: География,
автор: Лили11111111111111
Предмет: Физика,
автор: Tavkalot