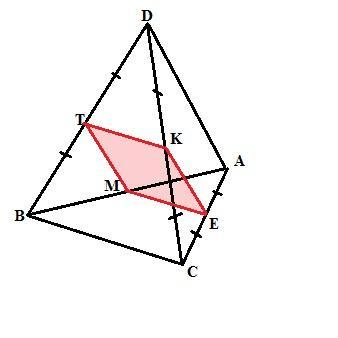
DABC-правельный тетраэдр. Точки T,K, и Е-середины ребер DB, DC и AC соответственно. Вычислите периметр сечения тетраэдра плоскостью TKE, если площадь грани тетраэдра равна 16√3 см³
Ответы
Ответ:
Ptkem = 16 см.
Объяснение:
В условии допущена описка.Площадь измеряется в кавдратных единицах, следовательно, площадь грани тетраэдра равна
S = 16√3 см².
Тетраэдр называется правильным, если все его грани - равносторонние треугольники. Тогда сторону тетраэдра найдем из формулы площади правильного треугольника:
S = (√3/4)*a², где а - сторона треугольника.
а² = 4*S/√3 = 4*16√3/√3 = 64 см² => a = 8см.
Точки T,K, и Е - середины ребер DB, DC и AC соответственно, следовательно, отрезки ТК и КЕ - средние линии треугольников - граней тетраэдра BDC и СDA и равны половинам сторон ВС и AD.
Построим сечение тетраэдра плоскостью ТКЕ. Плоскость BDC пересекается плоскостью TKE по линии ТК, параллельной прямой ВС. Но прямая ВС принадлежит и плоскости АВС. Следовательно, плоскость АВС пересечется плоскостью ТКЕ, проходящей через точку Е по прямой ЕМ, параллельной прямой ВС, а отрезок ЕМ является средней линией треугольника АВС. ЕМ = 4см. Соединив точки Т и М (середины сторон АВ и BD), получим сечение тетраэдра плоскостью ТКЕ - четырехугольник ТКЕМ, все стороны которого равны между собой и равны 4 см.
Периметр сечения Ptkem = 4*4 = 16 см.