Предмет: Алгебра,
автор: ata221
70 баллов! Помогите, пожалуйста, очень срочно! Умоляю.
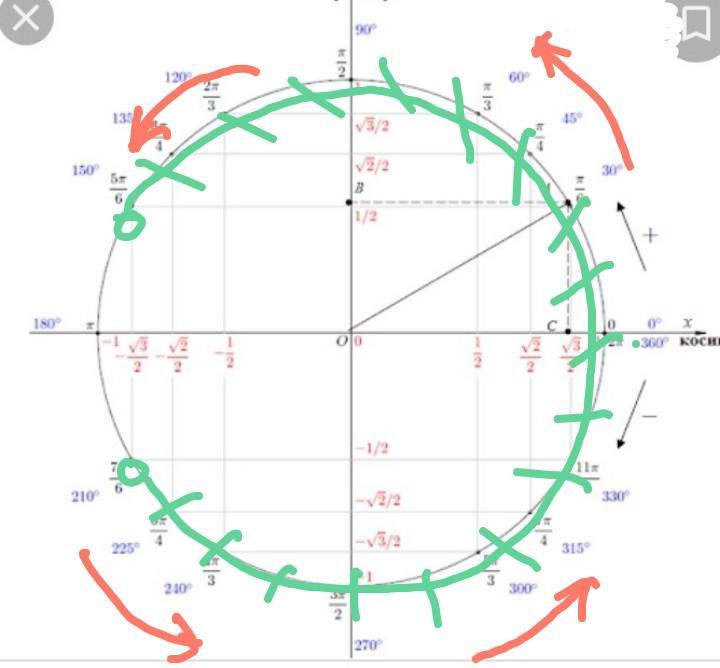
(В единичной окружности, направление указать вверх или вниз и т.д.)
Приложения:

Ответы
Автор ответа:
1
Ответ:
; k€Z
б)-7/18pi+2/3pik<x<pi/6+2/3pik; k€Z
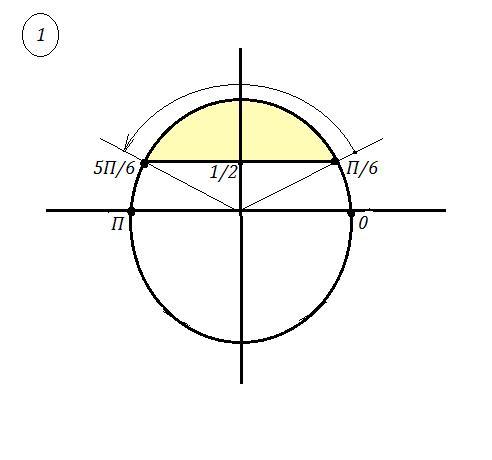
На чертеже показан первый шаг
работы ( решение неравенства до
алгебраических преобразований
и без учета периодичности).
Приложения:

Автор ответа:
2
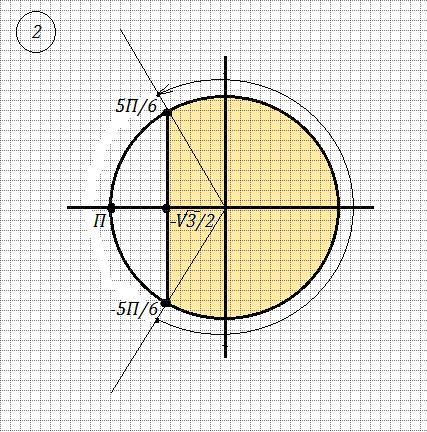
Ответ:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: zalina060819844
Предмет: Физика,
автор: ЕнотЕнотыч
Предмет: Биология,
автор: andrev17122001
Предмет: Алгебра,
автор: VeronikaTroll
Предмет: Математика,
автор: lenadzi1