Предмет: Алгебра,
автор: dasatotackaa
Помогите пожалуйста!!! Вычислите площадь фигуры ограниченной параболой у=-х²+4х-3, касательной к параболе в точке М(0;-3) и прямой х=2
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Площадь указанной фигуры находится по формуле Ньютона-Лейбница с непосредственным участием первообразных.
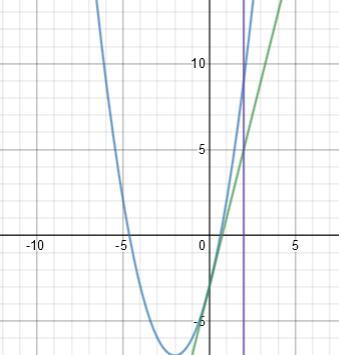
Касательная и парабола касаются в точке (0; -3), значит, касательная имеет вид y = 4x-3 (смотри чертеж).
Для данных кривых фигура имеет три общие точки: точка касания (0; -3), точка пересечения параболы и х=2 - точка (2; 9) и точка пересечения прямой y=4x-3 и прямой х=2 - точка (2; 5).
Имеем
.
Приложения:

Похожие вопросы
Предмет: Химия,
автор: AlisNK
Предмет: Русский язык,
автор: 5372292
Предмет: Математика,
автор: reaper13nik
Предмет: Алгебра,
автор: nastianad02
Предмет: Химия,
автор: Satenik22