Предмет: Алгебра,
автор: vityamath
Найдите период функции:
Приложения:
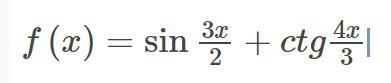
Ответы
Автор ответа:
3
Ответ:
/ - дробь.
f(x) = sin(3x/2) + ctg(4x/3).
Поделим данную функцию на две части:
sin(3x/2) и ctg(4x/3). Определим период каждой части,
Для функции sin(3x/2) подходит формула a×sin(bx+c). Периодом здесь будет P = 2π/B = 2π / 3/2 = 4π/3.
Для функции ctg(4x/3) подходит формула a×cot(bx+c). Периодом здесь будет P = π/B = π/ 4/3 = 3π/4.
Чтобы найти период функции из этих двух частей необходимо найти НОК(наименьшее общее кратное).
P1 = 4π/3 = 2×2×π×⅓.
P2 = 3π/4 = 3×π×¼.
Здесь это будет число 12π и соответственно, период функции f(x) = sin(3x/2) + ctg(4x/3) равен 12π.
vityamath:
Спасибо.
Похожие вопросы
Предмет: Русский язык,
автор: lexvasiljew
Предмет: Математика,
автор: melikova118
Предмет: Английский язык,
автор: swsвиктория1601
Предмет: Математика,
автор: batyademon
Предмет: География,
автор: Кискаk