Предмет: Алгебра,
автор: melihovadara82
Решите,пожалуйста, определенный интеграл
Приложения:
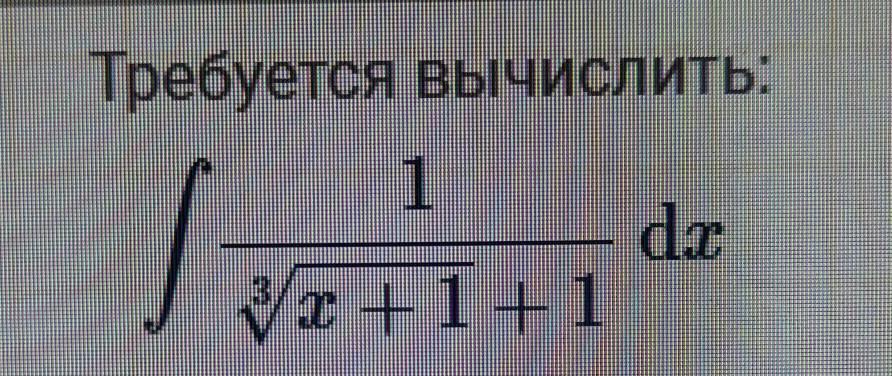
Simba2017:
и где же он определенный?
пардон, не указала,но я уже решила)
уберите вопрос тогда
не поскажите как его убрать?
Ответы
Автор ответа:
1
Ответ:
Замена:
От замены:
Похожие вопросы
Предмет: Математика,
автор: bmim69
Предмет: Литература,
автор: shilova1
Предмет: Математика,
автор: doneckova
Предмет: Геометрия,
автор: blaccyee0666
Предмет: Математика,
автор: Aigerusha26