Предмет: Алгебра,
автор: Динка2004
Помогите пожалуйста с четырьмя примерами!
Очень надо!
Приложения:
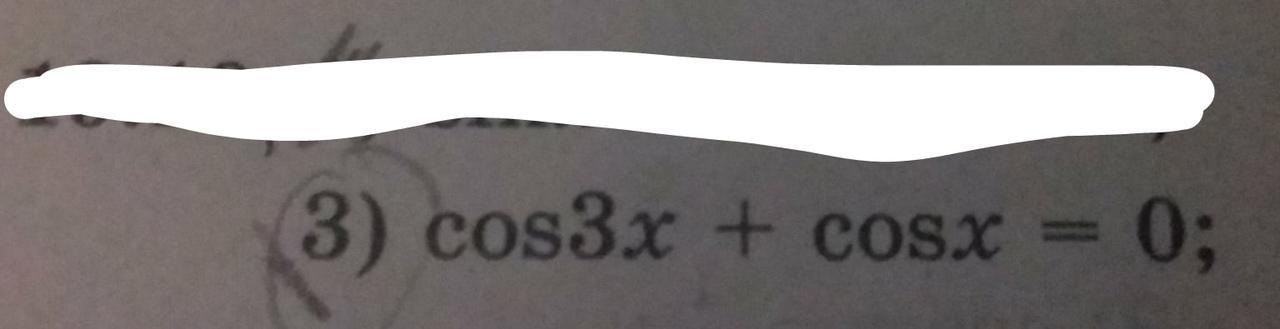
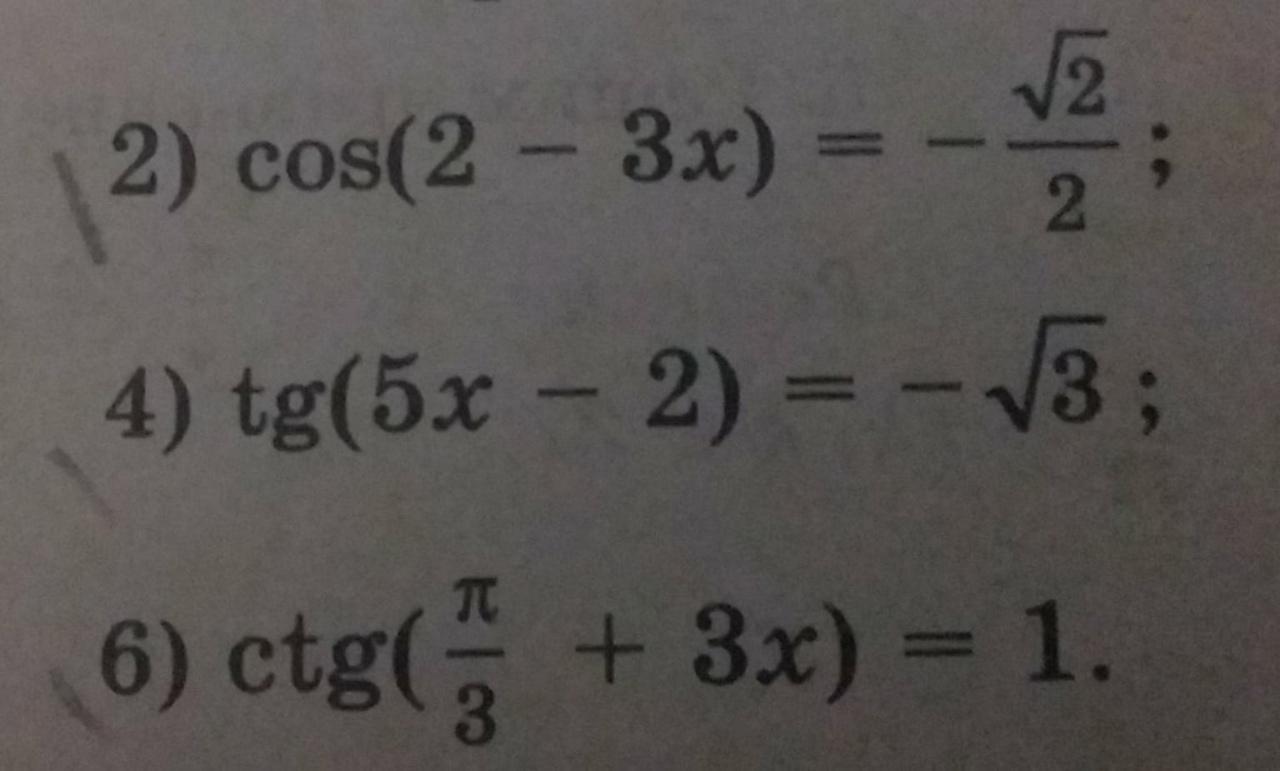
Ответы
Автор ответа:
1
Ответ:
везде n принадлежит Z.
ata221:
https://znanija.com/task/40742927 помогите, пожалуйста, очень Вас прошу!
Похожие вопросы
Предмет: Алгебра,
автор: Айгуль321
Предмет: Математика,
автор: vero4nik
Предмет: Русский язык,
автор: lena1285
Предмет: Литература,
автор: ШЕРШМИПС
Предмет: Математика,
автор: ibragimka277