Предмет: Математика,
автор: Wizard2222
Найти значение производной функции f(x) в точке x0
Приложения:
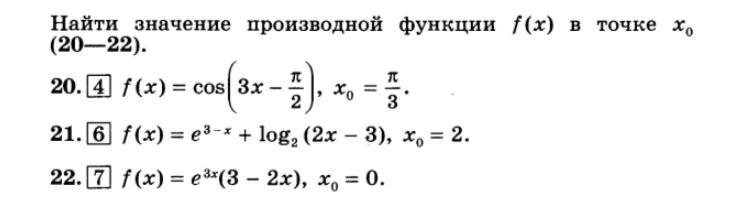
Ответы
Автор ответа:
2
Ответ:
Автор ответа:
1
Ответ:
20.
21.
22.
Пошаговое объяснение:
20.
f'(x)=(sin3x)'=3cos(3x)
21.
22.
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: schilinama
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: waloa
https://znanija.com/task/40727838