Предмет: Алгебра,
автор: meyfellovey
Помогите, пожалуйста, решить примеры по математике.
Приложения:

Ответы
Автор ответа:
1
Ответ:
разделим на cos(2x), не равный 0.
n принадлежит Z.
n принадлежит Z.
разделим на косинус в квадрате, не равный 0.
замена:
n принадлежит Z.
n принадлежит Z.
meyfellovey:
Спасибо огромное за помощь!
Автор ответа:
1
Ответ:
Надеюсь чем-то помогла. Извини, если не то, что надо
Приложения:
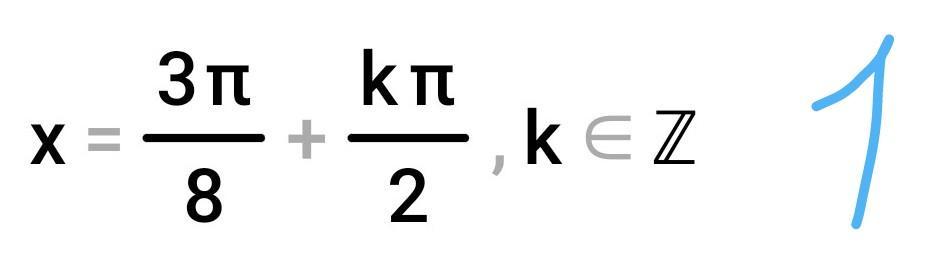
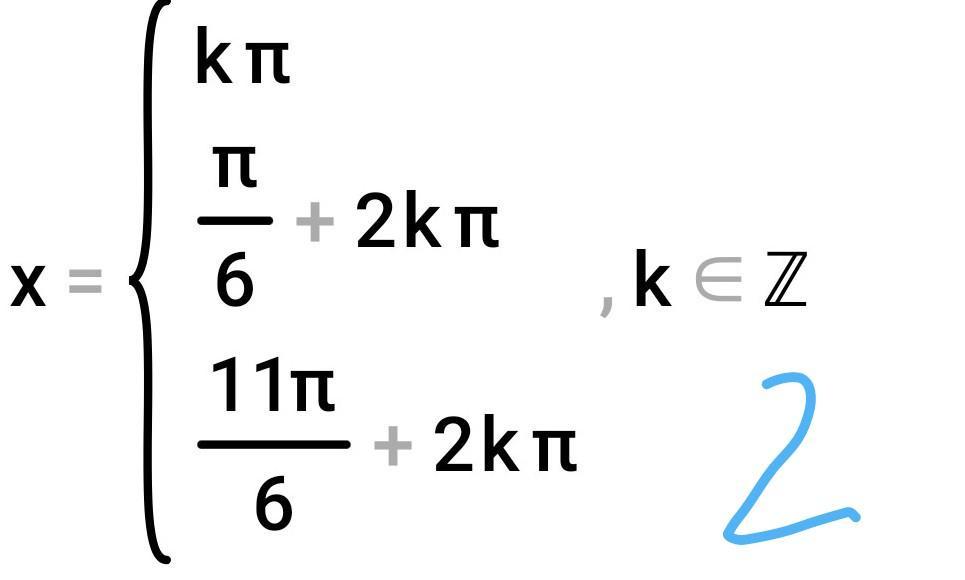

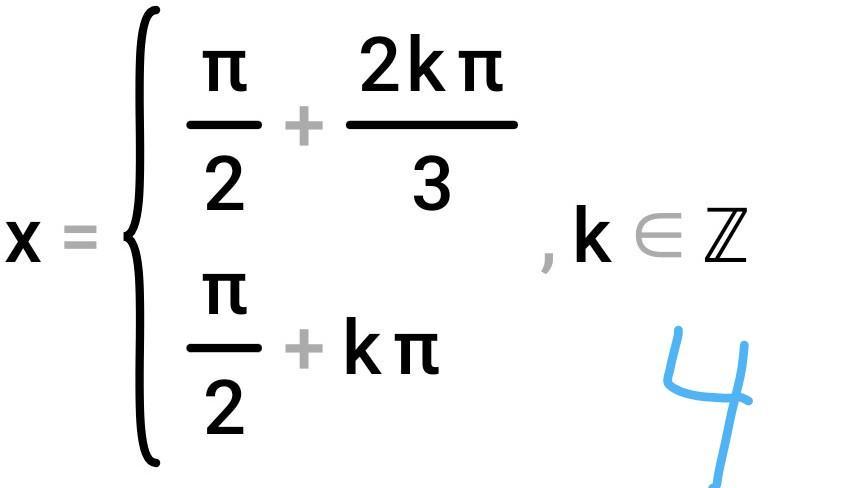
Спасибо большое за вашу помощь!
Похожие вопросы
Предмет: Математика,
автор: katyaponomarevva
Предмет: Русский язык,
автор: evenikitina20
Предмет: История,
автор: musencka
Предмет: Физика,
автор: никита3491
Предмет: Химия,
автор: Ivanov200300000