Предмет: Алгебра,
автор: VladislavSa
ДАЮ 15, НАЙТИ ПРОИЗВОДНУЮ
Приложения:
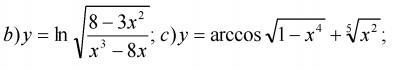
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Математика,
автор: Lola122444
Предмет: Русский язык,
автор: kolpakova12108
Предмет: Математика,
автор: hammbones
Предмет: Математика,
автор: davitvardanyan
Предмет: Биология,
автор: werty17