Question

найти наибольшее и наименьшее значение функции на промежутке [0;π/2]

Answer 1

Ответ:

Наибольшее $\frac{\sqrt{3}}{2}$

Наименьшее $-\frac{1}{2}$

Пошаговое объяснение:

Наибольшее значение функция принимает в правой границе отрезка - при $x=\frac{\pi}{2}$:

$y(\frac{\pi }{2} )=sin(\frac{\pi }{2} -\frac{\pi }{6} )=sin\frac{\pi }{3} =\frac{\sqrt{3} }{2}$

Наименьшее значение функция принимает в левой границе промежутка - при $x=0$:

$y(0)=sin(0-\frac{\pi }{6})=sin(-\frac{\pi }{6} )=-\frac{1}{2}$

Answer 2

Ответ:

Наименьшее значение функции на промежутке [0;π/2]: -0,5

Наибольшее значение функции на промежутке [0;π/2]: $\displaystyle \frac{\sqrt{3}}{2}$

Пошаговое объяснение:

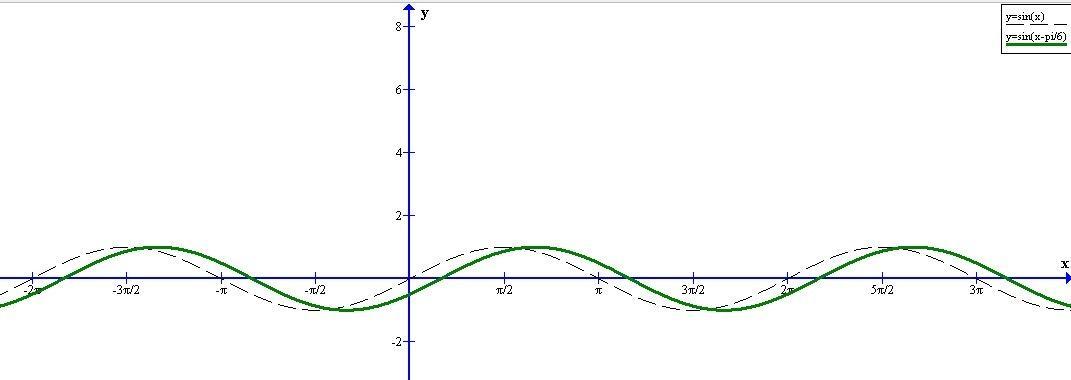
Видно, что наименьшее значение этой функции на промежутке [0;π/2] находится в точке с аргументом "0"

Если подставить значение аргумента "0" в формулу графика то мы получим значение: sin(-π/6)=-0,5

Это и есть наименьшее значение функции на промежутке [0;π/2].

Также видно, что наибольшее значение функции на промежутке [0;π/2] находится в точке с аргументом "π/2"

Поставим в формулу вместо "х" чтобы найти значение функции при значении аргумента "π/2"

$\displaystyle sin \left( \frac{\pi}{2} - \frac{\pi}{6} \right) = sin \left( \frac{3\pi - \pi}{6} \right) = sin \left(\frac{2\pi}{6} \right) = sin \left( \frac{\pi}{3} \right) = \frac{ \sqrt{3} }{2}$