Question

Из точки, отстоящей от плоскости на расстояние 1 м, проведены две равные наклонные. Найдите расстояние между основаниями наклонных, если известно, что наклонные перпендикулярны и образуют с перпендикуляром к плоскости углы, равные 60° Если возможно,то пожалуйста с рисунком=)

Answer 1

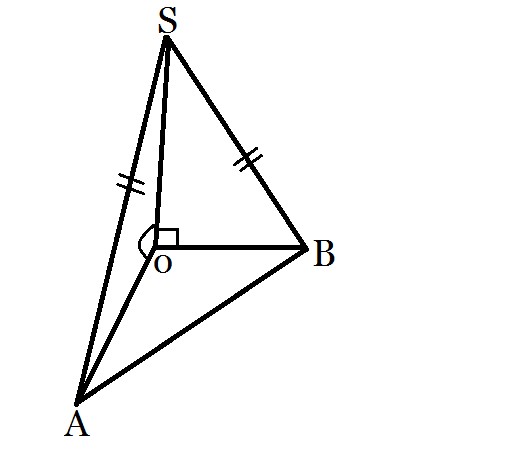
Пусть SA = SB данные наклонные, SO - перпендикуляр к плоскости, SO = 1м.

ΔAOS = ΔBOS - прямоугольные (по гипотенузе и острому углу)

∠ASO = 60 градусам и ∠BSO = 60 градусам, а, значит, ∠SAO = ∠SBO = 30 градусам

Поэтому:

SO = 1/2 SA = 1/2 SB. Так что SB = SA = 2м.

По условию SA ⊥ SB, тогда, по теореме Пифагора, получаем:

АВ = √SA(квадрат)+SB(квадрат) = √4+4 = √8 = 2√2 (м)