Предмет: Математика,
автор: MolkyWay
РЕБЯТА!!!! ПОМОГИТЕ!!! ПОЖАЛУЙСТА!!! СРОЧНО!!!
Приложения:
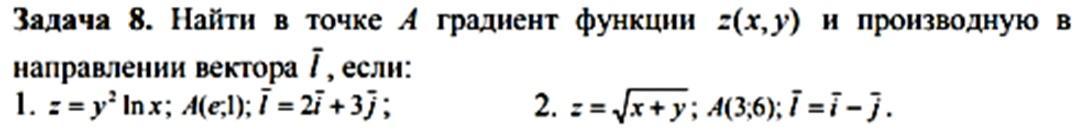
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
градиент это вектор, координатами которого являются частные производные данной функции, т.е.:
1) z=y²lnx
теперь посчитаем градиент в точке А
направление вектора-градиента задаётся его направляющими косинусами:
вычислим сначала модуль градиента а потом направляющие косинусы вектора градиента
теперь будем разбираться с производной
ищем производную в точке А по направлению вектора a(2;3)
и для вектора имеем
2) писанины много, поэтому здесь уже без теории, только расчеты
теперь производная в точке А по направлению вектора а = (1;1)
MolkyWay:
Ого!!! Спасибо)
Похожие вопросы
Предмет: Алгебра,
автор: aklbek
Предмет: Русский язык,
автор: pashavasilishi
Предмет: Химия,
автор: kolokol705
Предмет: История,
автор: elinaka45