Предмет: Математика,
автор: MolkyWay
ДРУЗЬЯ! ПОМОГИТЕ!!! СРОЧНО!
Приложения:
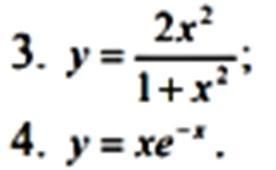
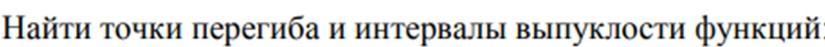
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
выпуклость и вогнутость, а также точки перегиба ищем при помощи второй производной
1)
это есть точки перегиба
имеем три интервала. на каждом выбираем любую точку и смотрим на знак производной в этой точке, а значит и на всем интервале
(-∞; -√3/3) у" < 0 ⇒ функция выпукла
(-√3/3; √3/3) у">0 ⇒ функция вогнута
(√3/3; +∞) у" < 0 ⇒ функция выпукла
2)
(-∞; 2) у" < 0 ⇒ функция выпукла
(2; +∞) у">0 ⇒ функция вогнута
Похожие вопросы
Предмет: Английский язык,
автор: polina21062004
Предмет: История,
автор: 6rose
Предмет: Литература,
автор: тим8
Предмет: Математика,
автор: sayfifap03d70