Предмет: Алгебра,
автор: pashagutorov00
варианте найти общий интеграл дифференциального уравнения:
Приложения:
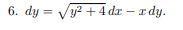
Ответы
Автор ответа:
1
Ответ:
общее решение.
djdjdjrk:
Помогите пожалуйста) https://znanija.com/task/40719479?utm_source=android&utm_medium=share&utm_campaign=question
Похожие вопросы
Предмет: Русский язык,
автор: oksanka100382
Предмет: Қазақ тiлi,
автор: nastyarodionov
Предмет: Русский язык,
автор: Angelina9807
Предмет: Математика,
автор: Gigoshkin1
Предмет: Математика,
автор: вованоджи