Предмет: Геометрия,
автор: bolshoibratsleditzat
Если можно, то с решением. Заранее спасибо. 50 баллов
Через катет АС прямоугольного треугольника АВС
(∠С=90°) проведена плоскость α под углом 60° к плоскости треугольника. Вычислите расстояние от вершины В к плоскости α , если АС=3 см и АВ= 2√3 см.
Ответы
Автор ответа:
1
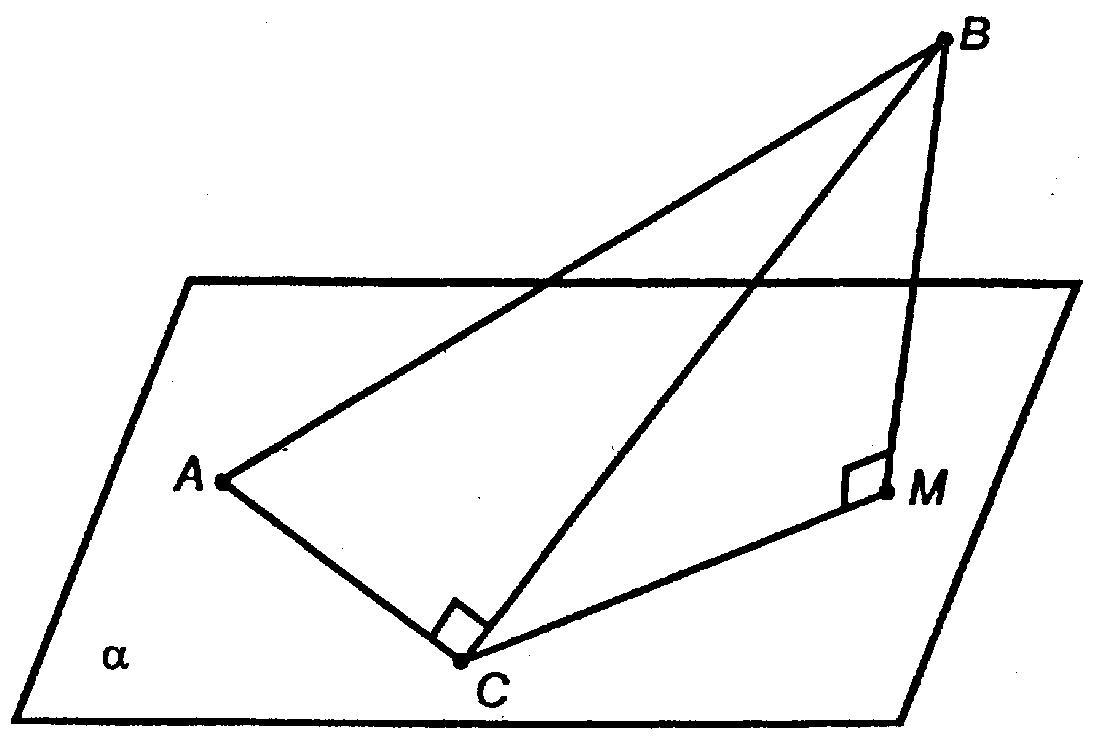
Дано:
ΔABC, AC⊂α, ∠C = 90°, ∠(α;(ABC)) = 60°, АС=3 см, АВ= 2√3 см
Найти:
BM - ?
Решение:
Проведем ВМ ⊥ α.
ВМ ⊥ α }
ВС - наклонная } ⇒ АС ⊥ МС (то по теореме, обратной к теореме о 3-х
АС ⊥ ВС } перпендикулярах).
∠ВСМ - линейный угол двугранного угла ВАСМ.
∠(α;(ABC)) = ∠MCB = 60° ρ(B,α) = BH
Из ΔАВС:
AB² = AC² + BC² - Теорема Пифагора
BC = √AB² - AC² = √(2√3 см)² - (3 см)² = √12 см² - 9 см² = √3 см² = √3 см
ΔBMC - прямоугольный ⇒ sin∠MCB = BM/BC ⇒ BM = BC×sin∠MCB
BM = √3 см × sin60° = √3 см × √3/2 = (√3)²/2 см = 3/2 см = 1,5 см
Ответ: BM = 1,5 см
Приложения:
bolshoibratsleditzat:
Спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: дракулаура456
Предмет: Физика,
автор: Дженафае
Предмет: Математика,
автор: anna6664cjvff
Предмет: География,
автор: Jdjejxi
Предмет: Литература,
автор: Tdugcv