Предмет: Математика,
автор: xgdewl
помогите пожалуйста умоляю)
Приложения:
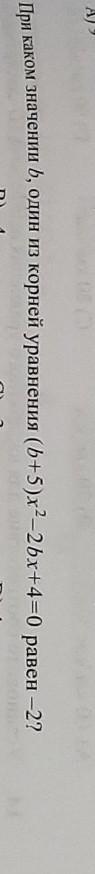
Ответы
Автор ответа:
0
Ответ:
Если b= -3
Надеюсь правильно.
Приложения:

Автор ответа:
0
Ответ:
Пошаговое объяснение:
ОДЗ:
Решение:
Решаем уравнение по теореме Виета:
По условию, один из корней уравнения равен –2:
Проверка:
Корни x₁ и x₂ совпали ⇒ b найдено верно.
Похожие вопросы
Предмет: Русский язык,
автор: karavanmobi
Предмет: История,
автор: nastasiKr1
Предмет: История,
автор: elazeylisg
Предмет: Литература,
автор: tamaralysykova
Предмет: Биология,
автор: yoonnie4138