Question

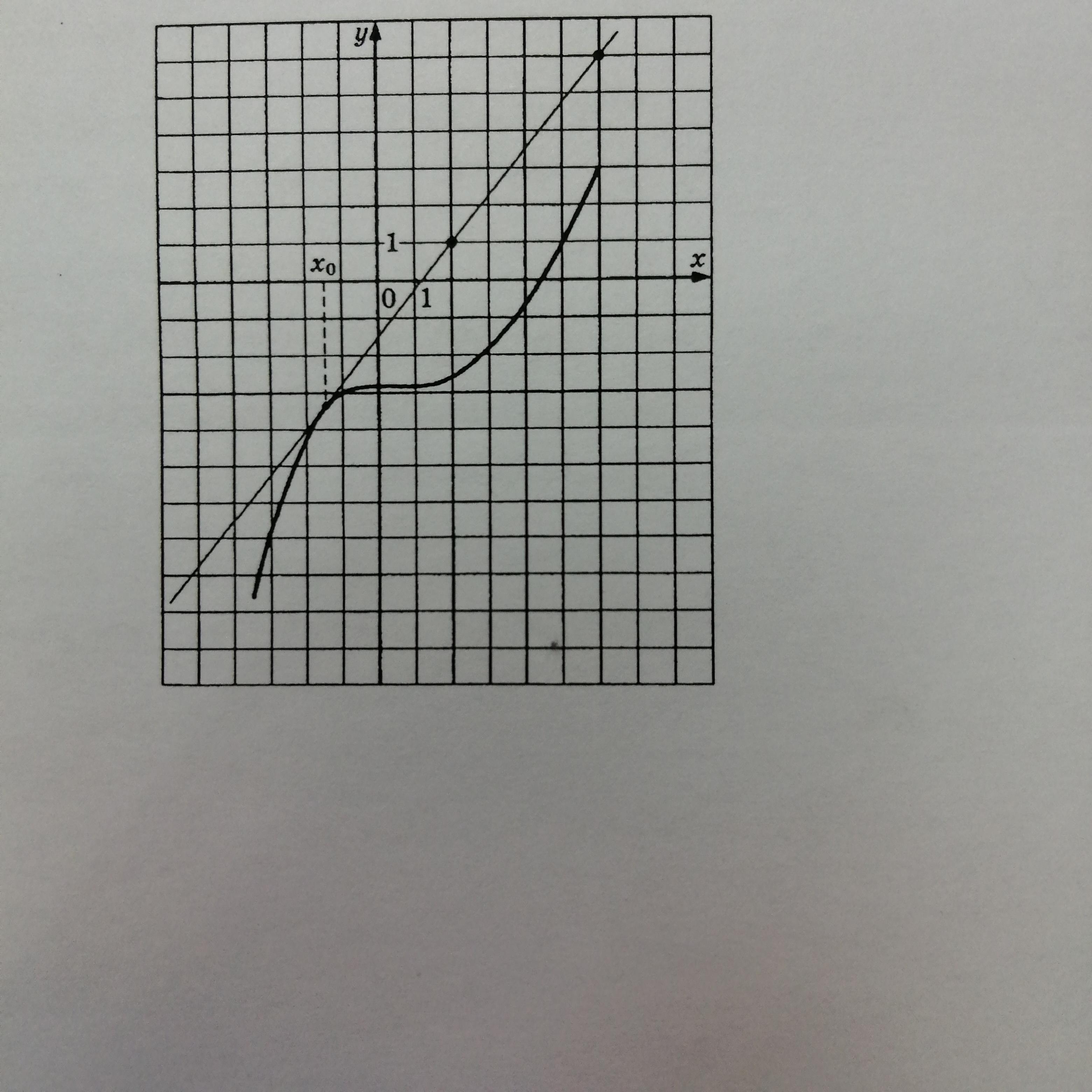
на рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x∨0. Найдите значение производной функции f(x) в точке x∨0

Answer 1

Ответ:

f'(x0)=1,25

Пошаговое объяснение:

f'(x0)=tg a=k

$tg \alpha = \frac{a}{b}$

a=5

b=4

$tg \alpha = \frac{5}{4}$

f'(x0)=1,25

Answer 2

Ответ:

Пошаговое объяснение:

по определению значение производной в точке х₀ есть tg угла наклона к ОХ касательной в этой точке

с другой стороны, если касательная задана как  у=ах+b, то а - это так же есть tg угла наклона к ОХ касательной, проведенной в точке х₀

из этих рассуждений выходит, что нам надо найти уравнение касательной. для этого у нас есть две точки (0;-1,5) и (5;6)

строим канонической а потом переходим к уравнению  прямой с угловым коэффициентом:

у=1,25x -1,5

отсюда получаем, что tg(х₀) = 1.25   ⇒  f'(х₀)= 1.25