Предмет: Алгебра,
автор: kiruxa124
помогите решить пожалуйста, 10 класс неравенства с модулями
Приложения:
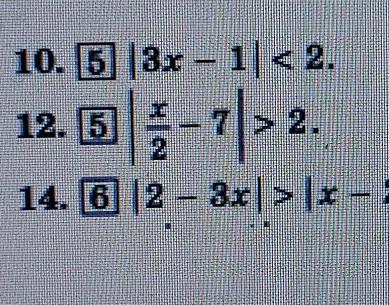
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Математика,
автор: eeoneguymchens
Предмет: Қазақ тiлi,
автор: darigasailaubek
Предмет: Математика,
автор: bunkowavika
Предмет: Музыка,
автор: zm65
Предмет: Математика,
автор: yulyagaevskayaoz1uaa