Предмет: Математика,
автор: ZoVV
Доказать что лимит не иснует
Приложения:
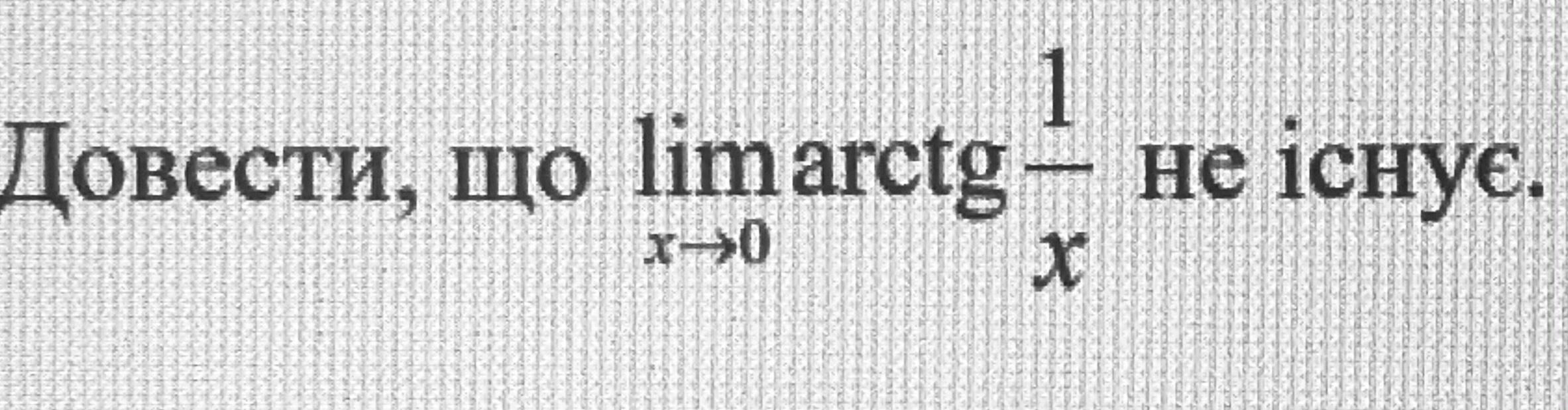
Ответы
Автор ответа:
1
Функция определена в
и
для сколь угодно малых
.
Тогда воспользуемся теоремой о связи двустороннего предела с односторонними: .
Односторонние пределы не равны, следовательно двустороннего не существует. Что и требовалось доказать.
Похожие вопросы
Предмет: Математика,
автор: arinka200505
Предмет: Английский язык,
автор: 1112233445566778899
Предмет: История,
автор: arina865
Предмет: Математика,
автор: натали200652