Предмет: Алгебра,
автор: moshimoshii
Уровень 11 класса (или немножко повыше)
Условие:
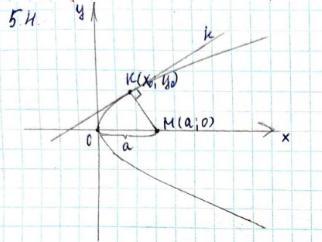
На оси параболы у дана точка М на расстоянии а от вершины. Найти абсциссу ближайшей к ней точки кривой. Чертёж прилагается.
дана точка М на расстоянии а от вершины. Найти абсциссу ближайшей к ней точки кривой. Чертёж прилагается.
Знаю, что нужно вывести формулу для отрезка МК и найти минимальное значение через производную. МК, скорее всего, можно найти как длину вектора МК(х0-а; у0)
Приложения:
LFP:
у0=+/- корень из (2рх0) второе значение ординаты можно не рассматривать (отрицательное --это для симметричной точки) и расстояние запишется как функция от икс (без нуля): корень квадратный из суммы квадратов координат вектора МК (или КМ): корень из ( (х-а)^2 + 2рх )
осталось продифференцировать
2х + (2р-2а) = 0
х0 = а-р
Ответы
Автор ответа:
1
Ответ:
точка на оси параболы может находиться или внутри или снаружи. если снаружи, то расстояние до вершины -кратчайшее и равно а.
если внутри, то необходимо найти минимум функции: f(x)=(a - x)^2+2px
и при приравнивании производной 0 получаем, что x=a-p.
Объяснение:
Правильно
Ошибка в записи функции: f(x)=(a - x)^2+2px, забыли про корень. Надо: f(x) = ((a - x)^2+2px)^(1/2).
Похожие вопросы
Предмет: Английский язык,
автор: шкальникк
Предмет: Английский язык,
автор: galionthik2010
Предмет: Математика,
автор: Shefishim
Предмет: Математика,
автор: ками120
Предмет: Математика,
автор: Аноним