Question

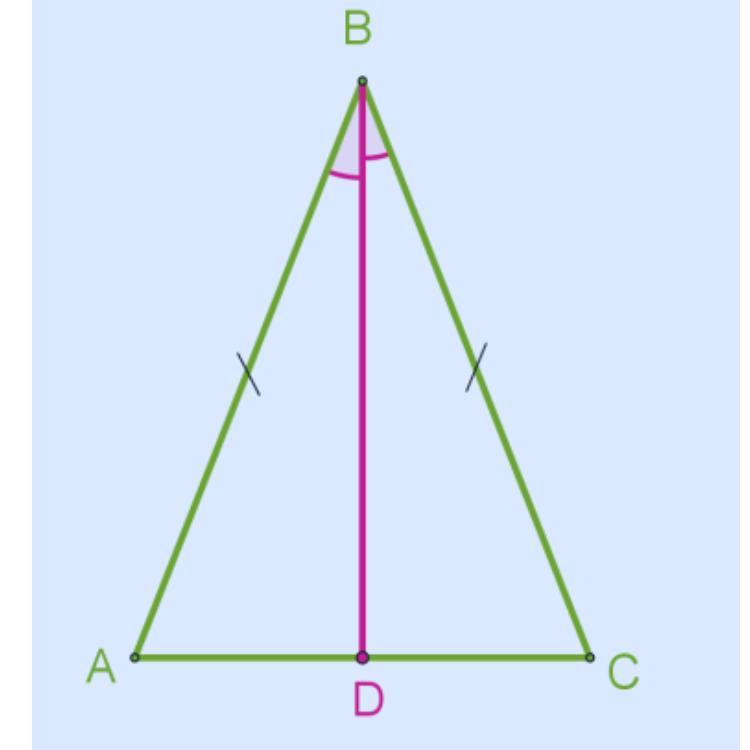
В равнобедренном треугольнике с длиной основания 41 cм проведена биссектриса угла ∡. Используя второй признак равенства треугольников, докажи, что отрезок является медианой, и определи длину отрезка .

Pazime22.png

Рассмотрим треугольники Δ и Δ (треугольник записать в алфавитном порядке);

1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡ = ∡ ;

2. так как проведена биссектриса, то ∡ = ∡ ;

3. стороны = у треугольников Δ и Δ равны, так как данный Δ — .

По второму признаку равенства треугольников Δ и Δ равны.
Значит, равны все соответствующие элементы, в том числе стороны =. А это означает, что отрезок является медианой данного треугольника и делит сторону пополам.

= см.

Answer 1

Ответ:

мало информации, глаза разбегаются, напишу, что знаю.

Объяснение:

Биссектриса угла АВС

АВD и CBD

1)BAD = BCD

2)ABD = CBD

3)AB BC; равнобедренный

4)ABD и CBD

AD и CD