Предмет: Математика,
автор: olgmakk3
Решите уравнение и найдите сумму его корней: х(х+3)(х+5)(х+8)=-56
Ответы
Автор ответа:
1
Ответ:
Вот
Пошаговое объяснение:
Приложения:
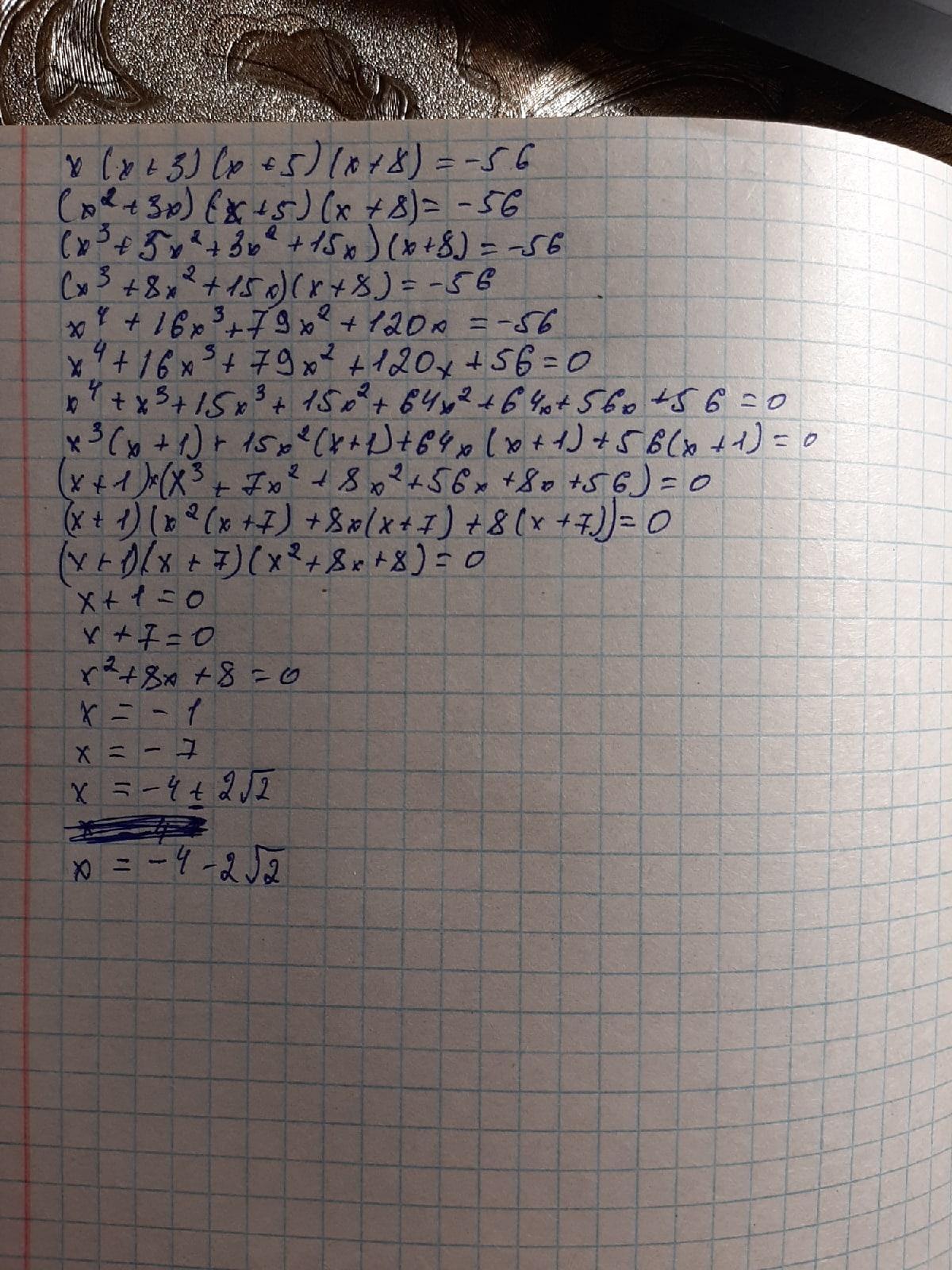
Автор ответа:
3
х(х+3)(х+5)(х+8)=-56
х(х+8)(х+3)(х+5)=-56
(x² + 8x)(x² + 8x + 15) + 56 = 0
x² + 8x = t
t(t + 15) + 56 = 0
t² + 15t + 56 = 0
D = 15² - 4*56 = 225 - 224 = 1
t12 = (-15 +- 1)/2 = -8 -7
1. t1 = -7
x² + 8x + 7 = 0
D = 64 - 28 = 36
x12 = (-8 +- 6)/2
x1 = -1
x2 = -7
2. t2 = -8
x² + 8x + 8 = 0
D = 64 - 32 = 32 = 16*2
x34 = (-8 +- 4√2)/2 = -4 +- 2√2
x3 = -4 + 2√2
x4 = -4 - 2√2
Сумма корней = -1 + (-7) + (-4 + 2√2) + (-4 - 2√2) = -16
==========
ну можно замену y = (0 + 3 + 5 + 8)/4 + x = x + 4
тогда
(y - 4)(y - 1)(y + 1)(y + 4) = -56
(y² - 1)(y² - 16) = -56
y² - 1 = t
t(t - 15) = -56 ......... итд
Похожие вопросы
Предмет: Физика,
автор: jojoi
Предмет: Русский язык,
автор: sofokotik2003
Предмет: Русский язык,
автор: fatarovshan
Предмет: Математика,
автор: ВаЛеРа06